题目内容

20．若分式方程$\frac{1}{x-3}$+1=$\frac{a-x}{x-3}$有增根，则a的值是（　　）
A．4B．0或4C．0D．0或-4

分析 增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母x-3=0，得到x=3，然后代入整式方程算出a的值即可．

解答 解：方程两边同时乘以x-3得，1+x-3=a-x，
∵方程有增根，
∴x-3=0，解得x=3．
∴1+3-3=a-3，解得a=4．
故选A．

点评 本题考查了分式方程的增根，先根据增根的定义得出x的值是解答此题的关键．

练习册系列答案
相关题目
10．计算题
（1）$\frac{1}{2}$（$\sqrt{2}$+$\sqrt{3}$）-$\frac{3}{4}$（$\sqrt{2}$+$\sqrt{27}$）
（2）（5$\sqrt{3}$-2$\sqrt{5}$）2．
11．在Rt三角形ABC中，∠ACB=90°，∠A=30° CD⊥AB于点D，那么△ACD与△BCD的面积之比为3．
8．已知，如图1，四边形ABCD，∠D=∠C=90°，点E在BC边上，P为边AD上一动点，过点P作PQ⊥PE，交直线DC于点Q．
（1）当∠PEC=70°时，求∠DPQ；
（2）当∠PEC=4∠DPQ时，求∠APE；
（3）如图3，将△PDQ沿PQ翻折使点D的对应点D′落在BC边上，当∠QD′C=40°时，请直接写出∠PEC的度数，答：65°．
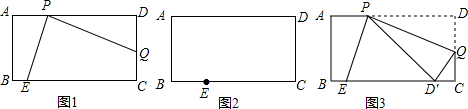
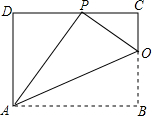15．如图，将矩形ABCD折叠，使得顶点B落在CD边上的P点处，折痕与边BC交于点O，AD=8，连结AP、OP、OA．
（1）求证：△ADP∽△PCO；
（2）若△OCP与△PDA的面积比为1：4，求边AB的长；
（3）若图中的点P恰好是CD边的中点，求∠OAB的度数．
5．已知⊙O1、⊙O2的半径分别为3、2，且⊙O1上的点都在⊙O2的外部，那么圆心距d的取值范围是d＞5或0≤d＜1．
12．解方程：
（1）2（3-y）=-4（y+5）；
（2）$\frac{3x-2}{4}$=$\frac{3}{8}$；
（3）$\frac{3x+4}{2}$-$\frac{7-2x}{12}$=1；
（4）x-$\frac{3-2x}{2}$=1-$\frac{x+2}{6}$．
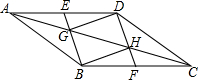9．如图，四边形ABCD是平行四边形，E、F分别是AD、BC中点，BE、DF分别交AC于G、H．求证：四边形GBHD是平行四边形．
10．已知关于x、y的方程组$\left\{\begin{array}{l}{2x-3y=3}\\{ax+by=-1}\end{array}\right.$和$\left\{\begin{array}{l}{3x+2y=11}\\{2ax+3by=3}\end{array}\right.$的解相同，求（3a+b）2012的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网