题目内容
5.已知⊙O1、⊙O2的半径分别为3、2,且⊙O1上的点都在⊙O2的外部,那么圆心距d的取值范围是d>5或0≤d<1.分析 据两圆的位置关系有相交、相切、相离,可得两圆的位置关系是相离,即外离或内含;再根据位置关系来判断其数量关系.
设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.
解答 解:∵⊙O1上的点都在⊙O2的外部,
∴它们的位置关系是外离或内含,
∴它们的圆心距d的取值范围是d>5或0≤d<1,
故答案为:d>5或0≤d<1.
点评 本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法,属于基础定义或定理,难度不大.

练习册系列答案
相关题目
20.若分式方程$\frac{1}{x-3}$+1=$\frac{a-x}{x-3}$有增根,则a的值是( )
| A. | 4 | B. | 0或4 | C. | 0 | D. | 0或-4 |
17.下列二次根式中与其他三个不是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{98}$ | C. | $\sqrt{50}$ | D. | $\sqrt{48}$ |
15.下列命题中,其逆命题是真命题的是( )
| A. | 对顶角相等 | |
| B. | 若a=b,则a2=b2 | |
| C. | 等三角形对应角相等 | |
| D. | 直角三角形两条直角边的平方和等于斜边的平方 |
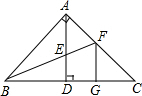 如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,BF平分∠ABC,交AD于E,FG∥AD.
如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,BF平分∠ABC,交AD于E,FG∥AD.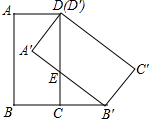 如图,在矩形ABCD中,BC=1,将矩形ABCD绕点D逆时针旋转45°,得到矩形A′B′C′D′,点B′恰好落在BC的延长线上,边A′B′交边CD于点E.
如图,在矩形ABCD中,BC=1,将矩形ABCD绕点D逆时针旋转45°,得到矩形A′B′C′D′,点B′恰好落在BC的延长线上,边A′B′交边CD于点E.