题目内容
15.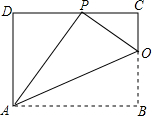 如图,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕与边BC交于点O,AD=8,连结AP、OP、OA.
如图,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕与边BC交于点O,AD=8,连结AP、OP、OA.(1)求证:△ADP∽△PCO;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长;
(3)若图中的点P恰好是CD边的中点,求∠OAB的度数.
分析 (1)由折叠的性质得到∠APO为直角,利用同角的余角相等得到一对角相等,再由一对直角相等,利用两对角相等的三角形相似即可得证;
(2)根据两三角形面积之比,确定出相似比,进而求出PC的长,设AB=x,表示出DP,利用勾股定理求出x的值,即可确定出AB的长;
(3)若P为CD中点,则有DP=PC=$\frac{1}{2}$DC,再由DC=AB,得到DP=$\frac{1}{2}$AP,进而确定出∠DAP度数,即可求出所求角度数.
解答 (1)证明:∵矩形ABCD,
∴∠B=∠D=∠C=90°,AB=CD,
由折叠可得∠APO=∠B=90°,AB=AP,
∴∠DPA+∠OPC=90°,
∵∠DAP+∠DPA=90°,
∴∠DAP=∠OPC,
∴△ADP∽△PCO;
(2)解:∵△ADP∽△PCO,且面积比为4:1,
∴相似比为2:1,即$\frac{AD}{PC}$=2,
∵AD=8,
∴PC=4,
设AB=DC=AP=x,则有DP=DC-PC=x-4,
在Rt△ADP中,根据勾股定理得:x2=82+(x-4)2,
解得:x=10,
则AB=10;
(3)∵P为DC中点,
∴PD=PC=$\frac{1}{2}$DC=$\frac{1}{2}$AB=$\frac{1}{2}$AP,
在Rt△ADP中,DP=$\frac{1}{2}$AP,
∴∠DAP=30°,
由折叠可得∠OAB=∠OAP,
∴∠OAB=30°.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,勾股定理,矩形的性质,以及折叠的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
5.函数y=$\frac{\sqrt{x-3}}{x-3}$中自变量x的取值范围正确的是( )
| A. | x>3 | B. | x≥3 | C. | x<3 | D. | x≤3 |
6.计算$\frac{a+5}{a-5}$•$\frac{a-5}{{a}^{2}+5a}$的结果是( )
| A. | $\frac{1}{a+5}$ | B. | $\frac{1}{a-5}$ | C. | $\frac{a+5}{a(a-5)}$ | D. | $\frac{1}{a}$ |
10.已知一次函数y=-2x+3,则与该一次函数的图象关于x轴对称的一次函数的表达式为( )
| A. | y=2x-3 | B. | y=-2x-3 | C. | y=2x+3 | D. | y=-2x+3 |
20.若分式方程$\frac{1}{x-3}$+1=$\frac{a-x}{x-3}$有增根,则a的值是( )
| A. | 4 | B. | 0或4 | C. | 0 | D. | 0或-4 |
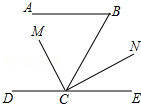 已知AB∥DE,∠B=68°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
已知AB∥DE,∠B=68°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.