题目内容
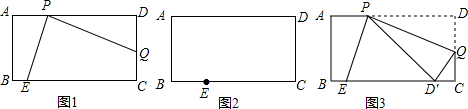
8.已知,如图1,四边形ABCD,∠D=∠C=90°,点E在BC边上,P为边AD上一动点,过点P作PQ⊥PE,交直线DC于点Q.(1)当∠PEC=70°时,求∠DPQ;
(2)当∠PEC=4∠DPQ时,求∠APE;
(3)如图3,将△PDQ沿PQ翻折使点D的对应点D′落在BC边上,当∠QD′C=40°时,请直接写出∠PEC的度数,答:65°.
分析 (1)由直角三角形两锐角互余和平角中挖去直角,余下的角互余∠APE+∠EPF=90°,计算即可;
(2)根据∠PEC=4∠DPQ求出,∠DPQ=18°,再和(1)方法一样计算;
(3)由对折的性质及∠QD′C=40°求出∠DPQ=40°,再和前面方法一样用互余计算即可.
解答 解:(1)如图,
作PF⊥BC,
∴∠PEF+∠EPF=∠APE+∠EPF=90°,
∵∠EPQ=90°,
∴∠APE+∠DPQ=90°,
∴∠EPF=∠DPQ,
∴∠PEF+∠DPQ=90°,
∵∠PEF=70°,
∴∠DPQ=20°.
(2)由(1)有,∠PEF+∠DPQ=90°,
∵∠PEC=4∠DPQ,
∴∠DPQ=18°,∠PEF=72°,
∵∠PEF+∠APE=90°,
∴∠APE=72°;
(3)∵∠C=∠D=90°,
∴∠QD′C+∠CQD′=90°,
∵∠QD′C=40°,
∴∠CQD′=50°,
由对折有,∠DQP=∠CQP,
∴∠DQP=$\frac{1}{2}$(180°-∠CQD')=65°,
∴∠DPQ=90°-∠DQP=25°,
由(1)有,∠PEC+∠DPQ=90°,
∴∠PEC=65°.故答案为65°.
点评 此题是几何变换综合题,主要考查了直角三角形中两锐角互余,折叠的性质,利用两锐角互余是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列各组数可以构成直角三角形的一组是( )
| A. | 3 5 6 | B. | 2 3 4 | C. | 6 7 9 | D. | 1.5 2 2.5 |
20.若分式方程$\frac{1}{x-3}$+1=$\frac{a-x}{x-3}$有增根,则a的值是( )
| A. | 4 | B. | 0或4 | C. | 0 | D. | 0或-4 |
17.下列二次根式中与其他三个不是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{98}$ | C. | $\sqrt{50}$ | D. | $\sqrt{48}$ |
18.下列生活现象中,属于平移的是( )
| A. | 足球在草地上滚动 | B. | 拉开抽屉 | ||
| C. | 电风扇风叶工作 | D. | 钟摆的摆动 |
 已知图为矩形,根据图中数据,则阴影部分的面积为8.
已知图为矩形,根据图中数据,则阴影部分的面积为8.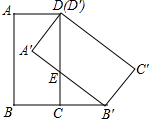 如图,在矩形ABCD中,BC=1,将矩形ABCD绕点D逆时针旋转45°,得到矩形A′B′C′D′,点B′恰好落在BC的延长线上,边A′B′交边CD于点E.
如图,在矩形ABCD中,BC=1,将矩形ABCD绕点D逆时针旋转45°,得到矩形A′B′C′D′,点B′恰好落在BC的延长线上,边A′B′交边CD于点E.