题目内容
9.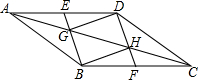 如图,四边形ABCD是平行四边形,E、F分别是AD、BC中点,BE、DF分别交AC于G、H.求证:四边形GBHD是平行四边形.
如图,四边形ABCD是平行四边形,E、F分别是AD、BC中点,BE、DF分别交AC于G、H.求证:四边形GBHD是平行四边形.
分析 由四边形ABCD是平行四边形,得到AD=BC,AD∥BC,得到DE=BF,推出四边形BFDE是平行四边形,根据平行四边形的性质得到BE=DF,证得△ADH≌△CBG,得到DH=BG,于是得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E、F分别是AD、BC中点,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE=DF,BE∥DF,
∴∠AHB=∠DGC,
∵∠DAG=∠BCH,
在△ADH与△CBG中,$\left\{\begin{array}{l}{∠DAH=∠BCG}\\{∠AHD=∠CGB}\\{AD=CB}\\{\;}\end{array}\right.$,
∴△ADH≌△CBG,∴DH=BG,
∵DH∥BG,
∴四边形GBHD是平行四边形.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定和性质,证明四边形BFDE是平行四边形是关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20.若分式方程$\frac{1}{x-3}$+1=$\frac{a-x}{x-3}$有增根,则a的值是( )
| A. | 4 | B. | 0或4 | C. | 0 | D. | 0或-4 |
17.下列二次根式中与其他三个不是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{98}$ | C. | $\sqrt{50}$ | D. | $\sqrt{48}$ |
4.下列说法正确的个数是( )
①同一平面内,过一点有且只有一条直线与已知直线垂直;
②同一平面内,过一点有且只有一条直线与已知直线平行;
③若三条直线a⊥c,b⊥c,则a∥b;
④9的平方根是3;
⑤-2是4的平方根;
⑥平方根等于本身的数是0和1.
①同一平面内,过一点有且只有一条直线与已知直线垂直;
②同一平面内,过一点有且只有一条直线与已知直线平行;
③若三条直线a⊥c,b⊥c,则a∥b;
④9的平方根是3;
⑤-2是4的平方根;
⑥平方根等于本身的数是0和1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列生活现象中,属于平移的是( )
| A. | 足球在草地上滚动 | B. | 拉开抽屉 | ||
| C. | 电风扇风叶工作 | D. | 钟摆的摆动 |
19. 为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?
为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?
(1)此次调查样本容量为300;
(2)在表中m=120; m=0.3;
(3)补全频数分布直方图.
 为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?
为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?| 分数段 | 步数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
(2)在表中m=120; m=0.3;
(3)补全频数分布直方图.
 已知图为矩形,根据图中数据,则阴影部分的面积为8.
已知图为矩形,根据图中数据,则阴影部分的面积为8. 在△ABC中,AB=3,AC=5,BC=7,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是3:5.
在△ABC中,AB=3,AC=5,BC=7,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是3:5.