题目内容
11.在Rt三角形ABC中,∠ACB=90°,∠A=30° CD⊥AB于点D,那么△ACD与△BCD的面积之比为3.分析 先根据题意判断出Rt△ABC∽Rt△CBD,再根据相似三角形的面积比等于相似比的平方进行解答即可.
解答 解:∵CD⊥AB,
∴∠BCD+∠B=90°,
∵∠A+∠B=90°,
∴∠A=∠BCD,
∵∠B=∠B,
∴Rt△ABC∽Rt△CBD,
∴$\frac{{S}_{△BCD}}{{S}_{△ABC}}$=($\frac{BC}{AB}$)2=(sin∠A)2=$\frac{1}{4}$,
∴$\frac{{S}_{△ACD}}{{S}_{△BCD}}$=3.
故答案为:3.
点评 本题考查的是相似三角形的判定与性质及直角三角形的性质,根据题意得出Rt△ABC∽Rt△CBD是解答此题的关键.

练习册系列答案
相关题目
6.计算$\frac{a+5}{a-5}$•$\frac{a-5}{{a}^{2}+5a}$的结果是( )
| A. | $\frac{1}{a+5}$ | B. | $\frac{1}{a-5}$ | C. | $\frac{a+5}{a(a-5)}$ | D. | $\frac{1}{a}$ |
20.若分式方程$\frac{1}{x-3}$+1=$\frac{a-x}{x-3}$有增根,则a的值是( )
| A. | 4 | B. | 0或4 | C. | 0 | D. | 0或-4 |
 已知图为矩形,根据图中数据,则阴影部分的面积为8.
已知图为矩形,根据图中数据,则阴影部分的面积为8.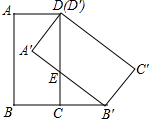 如图,在矩形ABCD中,BC=1,将矩形ABCD绕点D逆时针旋转45°,得到矩形A′B′C′D′,点B′恰好落在BC的延长线上,边A′B′交边CD于点E.
如图,在矩形ABCD中,BC=1,将矩形ABCD绕点D逆时针旋转45°,得到矩形A′B′C′D′,点B′恰好落在BC的延长线上,边A′B′交边CD于点E. 在△ABC中,AB=3,AC=5,BC=7,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是3:5.
在△ABC中,AB=3,AC=5,BC=7,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是3:5.