题目内容
3.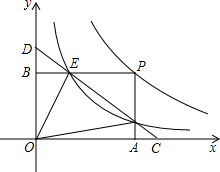 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )| A. | ①正确,②正确 | B. | ①正确,②错误 | C. | ①错误,②正确 | D. | ①错误,②错误 |
分析 根据反比例函数k的几何意义可对①解析判断;作EH⊥x轴于H,FG⊥y轴于G,如图,利用反比例函数图象上点的坐标特征设F(a,$\frac{k}{a}$),则P(a,$\frac{m}{a}$),E($\frac{ak}{m}$,$\frac{m}{a}$),再证明△DBE∽△DGF,利用相似比得到$\frac{DE}{DF}$=$\frac{BE}{GF}$=$\frac{k}{m}$,同样方法$\frac{CF}{CE}$=$\frac{AF}{EH}$=$\frac{k}{m}$,则$\frac{DE}{DF}$=$\frac{CF}{CE}$,然后利用比例性质可得DE=CF,则可对②进行判断.
解答 解:∵S△OBE=S△OFA=$\frac{1}{2}$k,S矩形PAOB=m,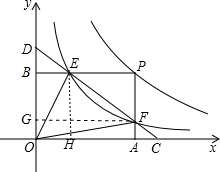
∴四边形OEPF的面积=S矩形PAOB-S△OBE-S△OFA=m-$\frac{1}{2}$k-$\frac{1}{2}$k=m-k,所以①正确;
作EH⊥x轴于H,FG⊥y轴于G,如图,
设F(a,$\frac{k}{a}$),则P(a,$\frac{m}{a}$),E($\frac{ak}{m}$,$\frac{m}{a}$),
∵BE∥FG,
∴△DBE∽△DGF,
∴$\frac{DE}{DF}$=$\frac{BE}{GF}$=$\frac{\frac{ak}{m}}{a}$=$\frac{k}{m}$,
∵AF∥AE,
∴△CAF∽△CHE,
∴$\frac{CF}{CE}$=$\frac{AF}{EH}$=$\frac{\frac{k}{a}}{\frac{m}{a}}$=$\frac{k}{m}$,
∴$\frac{DE}{DF}$=$\frac{CF}{CE}$,即$\frac{DE}{DE+EF}$=$\frac{CF}{CF+EF}$,
∴$\frac{DE}{EF}$=$\frac{CF}{EF}$,
∴DE=CF,所以②正确.
故选A.
点评 本题考查了反比例函数比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.判断②的关键是利用相似比,用k和m表示出$\frac{DE}{DF}$和$\frac{CF}{CE}$.

 考前必练系列答案
考前必练系列答案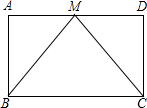 已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.
已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形. 在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求:
在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求: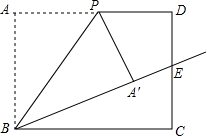 如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.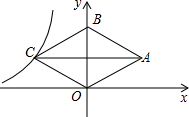 如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.
如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.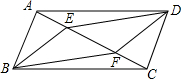 如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.