题目内容
13.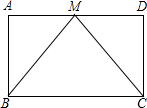 已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.
已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.
分析 由SSS证明△ABM≌△DCM,得出∠A=∠D,由平行线的性质得出∠A+∠D=180°,证出∠A=90°,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
在△ABM和△DCM中,$\left\{\begin{array}{l}{AM=DM}&{\;}\\{AB=DC}&{\;}\\{BM=CM}&{\;}\end{array}\right.$,
∴△ABM≌△DCM(SSS).
∴∠A=∠D.
∵AB∥CD,
∴∠A+∠D=180°.
∴∠A=90°.
∴?ABCD是矩形.
点评 此题主要考查了矩形的判定、平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等得出对应角相等是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
3.下列说法中,正确的有( )
①圆的半径垂直于弦;
②直径是弦;
③圆的内接平行四边形是矩形;
④圆内接四边形的对角互补;
⑤长度相等的两条弧是等弧;
⑥相等的圆心角所对的弧相等.
①圆的半径垂直于弦;
②直径是弦;
③圆的内接平行四边形是矩形;
④圆内接四边形的对角互补;
⑤长度相等的两条弧是等弧;
⑥相等的圆心角所对的弧相等.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
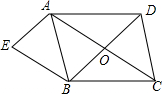 如图,在?ABCD中,对角线AC、BD相交于点O,AE∥BD,BE∥AC,AE与BE相交于点E,当AB,AD满足什么条件时,四边形AEBO为矩形?请说明埋由.
如图,在?ABCD中,对角线AC、BD相交于点O,AE∥BD,BE∥AC,AE与BE相交于点E,当AB,AD满足什么条件时,四边形AEBO为矩形?请说明埋由.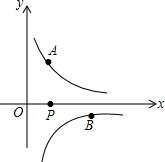 如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).
如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0). 如图,在?ABCD中,AE=CF,试说明EF,BD互相平分的理由.
如图,在?ABCD中,AE=CF,试说明EF,BD互相平分的理由.
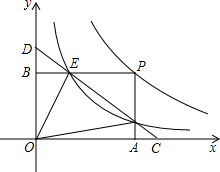 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )