题目内容
11.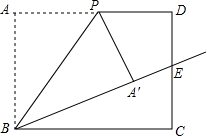 如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
分析 由矩形的性质得出AD=BC=12,CD=AB=10,∠A=∠D=∠C=90°,由勾股定理求出BE,由折叠的性质得出∠BAP′=∠A=90°,BA′=BA=10,PA′=PA,得出∠PA′E=90°,A′E=13-10=3,连接PE,设PA′=PA=x,则PD=12-x,由勾股定理得出方程,解方程求出PA′,得出PD,即可求出四边形DPA′E的面积.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=12,CD=AB=10,∠A=∠D=∠C=90°,
∵E是CD的中点,
∴DE=CE=5,
∴BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
由折叠的性质得:∠BAP′=∠A=90°,BA′=BA=10,PA′=PA,
∴∠PA′E=90°,A′E=13-10=3,
连接PE,如图所示:
设PA′=PA=x,则PD=12-x,
由勾股定理得:PE2=PA′2+A′E2=PD2+DE2,
即x2+32=(12-x)2+52,
解得:x=$\frac{20}{3}$,
∴PA′=$\frac{20}{3}$,PD=12-$\frac{20}{3}$=$\frac{16}{3}$,
∴四边形DPA′E的面积=$\frac{1}{2}×3×\frac{20}{3}$+$\frac{1}{2}$×5×$\frac{16}{3}$=$\frac{70}{3}$;
故答案为:$\frac{70}{3}$.
点评 本题考查了矩形的性质、折叠的性质、勾股定理;熟练掌握矩形和折叠的性质,由勾股定理求出PA′、PD是解决问题的关键.

练习册系列答案
相关题目
16.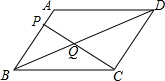 如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
 如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )| A. | 9 | B. | 11 | C. | 12 | D. | 14 |
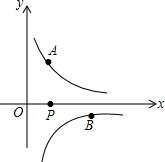 如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).
如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).
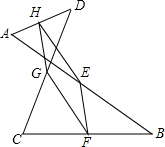 如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.
如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.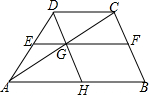 已知:如图,在?BCDH中,G是DH的中点,连接CG,CG与BH的延长线交于点A,连接AD,E是AD的中点,连接EG并延长交BC于点F,求证:GF=2EG.
已知:如图,在?BCDH中,G是DH的中点,连接CG,CG与BH的延长线交于点A,连接AD,E是AD的中点,连接EG并延长交BC于点F,求证:GF=2EG.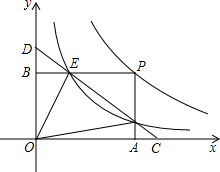 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )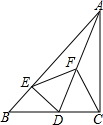 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.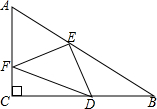 如图,在△ABC中,∠C=90°,∠B=30°,CB=4,点D是CB的中点,点E,F分别在AB,AC上,则△DEF的周长的最小值是2$\sqrt{7}$.
如图,在△ABC中,∠C=90°,∠B=30°,CB=4,点D是CB的中点,点E,F分别在AB,AC上,则△DEF的周长的最小值是2$\sqrt{7}$.