题目内容
12.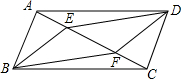 如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
分析 连接BD,根据平行四边形的性质可得BO=DO,再根据平行线的性质可得∠BEO=∠DFO,然后证明△BOE≌△DOF,可得EO=FO,可判定四边形BEDF是平行四边形,进而可得ED=BF.
解答 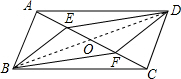 证明:连接BD,
证明:连接BD,
∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE∥DF,
∴∠BEO=∠DFO,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{∠BOE=∠DOF}\\{∠BEO=∠DFO}\\{BO=DO}\end{array}\right.$,
∴△BOE≌△DOF(AAS),
∴EO=FO,
∴四边形BEDF是平行四边形,
∴ED=BF.
点评 此题主要平行四边形的判定和性质,关键是掌握平行四边形对角线互相平分,对边相等.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
3.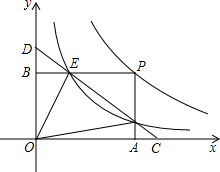 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )| A. | ①正确,②正确 | B. | ①正确,②错误 | C. | ①错误,②正确 | D. | ①错误,②错误 |
17.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A(-2,1),则当x<-1时,函数值y的取值范围是( )
| A. | y>2 | B. | -2<y<0 | C. | y>-2 | D. | 0<y<2 |

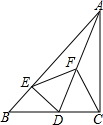 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.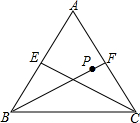 如图,在正△ABC中,CE、BF分别是边AB、AC上的中线,点P是BF上的一动点,若AB=6,则AP+PE的最小值为3$\sqrt{3}$.
如图,在正△ABC中,CE、BF分别是边AB、AC上的中线,点P是BF上的一动点,若AB=6,则AP+PE的最小值为3$\sqrt{3}$.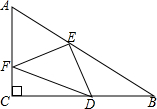 如图,在△ABC中,∠C=90°,∠B=30°,CB=4,点D是CB的中点,点E,F分别在AB,AC上,则△DEF的周长的最小值是2$\sqrt{7}$.
如图,在△ABC中,∠C=90°,∠B=30°,CB=4,点D是CB的中点,点E,F分别在AB,AC上,则△DEF的周长的最小值是2$\sqrt{7}$.