题目内容
8.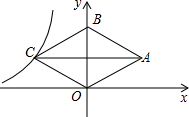 如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.
如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.
分析 先根据菱形的性质求出C点坐标,再把C点坐标代入反比例函数的解析式即可得出k的值.
解答 解:∵菱形的两条对角线的长分别是6和4,
∴C(-3,2),
∵点C在反比例函数y=$\frac{k}{x}$的图象上,
∴2=$\frac{k}{-3}$,
解得k=-6.
故答案为:-6.
点评 本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定满足此函数的解析式.

练习册系列答案
相关题目
18.已知反比例函数y=$\frac{k-1}{x}$的图象经过点(-2,1).
(1)求k的值;
(2)判断下列各点否在这个图象上(-0.5,2),(4,-0.5),($\frac{1}{3}$,-6)
(1)求k的值;
(2)判断下列各点否在这个图象上(-0.5,2),(4,-0.5),($\frac{1}{3}$,-6)
16.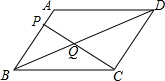 如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
 如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )| A. | 9 | B. | 11 | C. | 12 | D. | 14 |
3.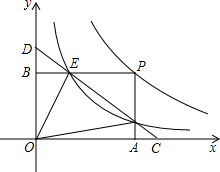 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )| A. | ①正确,②正确 | B. | ①正确,②错误 | C. | ①错误,②正确 | D. | ①错误,②错误 |
17.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A(-2,1),则当x<-1时,函数值y的取值范围是( )
| A. | y>2 | B. | -2<y<0 | C. | y>-2 | D. | 0<y<2 |
18. 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )
 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )| A. | △ODB与△OCA的面积相等 | |
| B. | 当点A是PC的中点时,点B一定是PD的中点. | |
| C. | 只有当四边形OCPD为正方形时,四边形PAOB的面积最大 | |
| D. | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
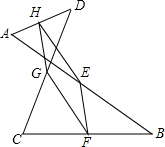 如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.
如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.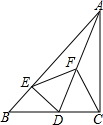 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.