题目内容
14. 在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求:
在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求:(1)AB边的长度.
(2)线段OE的长度.
(3)线段AF的长度.
分析 (1)由矩形的性质得出OA=OB=OD=OC,证出△AOB是等边三角形,得出AB=OA=4cm;
(2)由三角形中位线定理得出OE=$\frac{1}{2}$AB=2cm即可;
(3)由等边三角形的性质得出BF=$\frac{1}{2}$OB=2cm,由勾股定理求出AF即可.
解答 解:(1)∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC=4cm,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB=OD=OC,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=4cm;
(2)∵OB=OD,点E为AD边的中点,
∴OE=$\frac{1}{2}$AB=2cm;
(3)∵△AOB是等边三角形,
∴AB=OA=OB=4cm,
∵AF⊥BD,
∴BF=$\frac{1}{2}$OB=2cm,
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$(cm).
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理;熟练掌握矩形的性质,证明△AOB是等边三角形是解决问题的关键.

练习册系列答案
相关题目
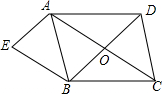 如图,在?ABCD中,对角线AC、BD相交于点O,AE∥BD,BE∥AC,AE与BE相交于点E,当AB,AD满足什么条件时,四边形AEBO为矩形?请说明埋由.
如图,在?ABCD中,对角线AC、BD相交于点O,AE∥BD,BE∥AC,AE与BE相交于点E,当AB,AD满足什么条件时,四边形AEBO为矩形?请说明埋由.
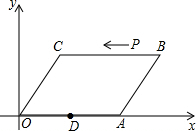 如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s
如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s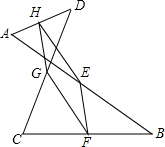 如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.
如图,E、F、G、H分别是线段AB、CB、CD、AD的中点,连接E,F,G,H,判断四边形EFGH的形状,并说明理由.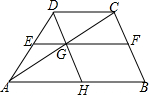 已知:如图,在?BCDH中,G是DH的中点,连接CG,CG与BH的延长线交于点A,连接AD,E是AD的中点,连接EG并延长交BC于点F,求证:GF=2EG.
已知:如图,在?BCDH中,G是DH的中点,连接CG,CG与BH的延长线交于点A,连接AD,E是AD的中点,连接EG并延长交BC于点F,求证:GF=2EG.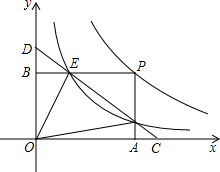 如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )
如图,点P是反比例函数y=$\frac{m}{x}$(x>0)图象上的一点,矩形OAPB的顶点A,B分别在x轴与y轴上,且边PB,PA分别交反比例函数y=$\frac{k}{x}$(x>0)的图象于E,F两点,直线EF交x轴于C点,交y轴于D点,连结OE,OF.现给出下列结论:①四边形OEPF的面积为m-k;②DE=CF.则( )