题目内容
5.在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.(1)如图1,若点E,F分别落在边AB,AC上,探索PC与PE的数量关系,并说明理由.
( 2)如图2、图3,把图1中的△AEF绕着点A顺时针旋转,点E落在边CA的延长线上(如图2);或者点F落在边AB上(如图3).其他条件不变,问题(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;
(3)记$\frac{AC}{BC}$=k,当k为何值时,△CPE总是等边三角形.

分析 (1)利用直角三角形斜边的中线等于斜边的一半,即可.
(2)①先判断△CBP≌△HPF,再利用直角三角形斜边的中线等于斜边的一半,②先判断△DAF≌△EAF,再判断△DAP≌△EAP,然后用比例式即可;
(3)先判断△CAE∽△CNP,再判断等腰△PCE∽等腰△NCA,即可.
解答 解:(1)PC=PE,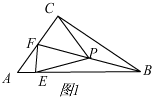
证明:∵∠ACB=∠AEF=90°
∴Rt△FCB和Rt△BEF
∵点P是BF的中点
∴CP=$\frac{1}{2}$BF,EP=$\frac{1}{2}$BF,
∴PC=PE;
(2)①如图2,延长CP、EF交于点H,PC=PE仍然成立
证明:∵∠ACB=∠AEF=90°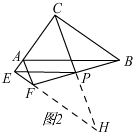
∴EH∥CB
∴∠CBP=∠PFH,∠H=∠BCP
∵点P是BF的中点
∴PC=PH
∴△CBP≌△HPF(AAS)
∴PC=PH,
∵∠AEF=90°
∴Rt△CEH中,EP=$\frac{1}{2}$CH,
∴PC=PE;
②如图3,过点F作FD⊥AC于点D,过点P作PM⊥AC于点M,连接PD,PC=PE成立,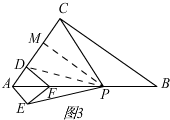
证明:∵∠DAF=∠EAF,∠FDA=∠FEA=90°,
在△DAF和△EAF中,
$\left\{\begin{array}{l}{∠DAF=∠EAF}\\{∠FDA=∠FEA}\\{AF=AF}\end{array}\right.$,
∴△DAF≌△EAF(AAS),
∴AD=AE,
在△DAP和△EAP中,
$\left\{\begin{array}{l}{AD=AE}\\{∠DAP=∠EAP}\\{AP=AP}\end{array}\right.$,
∴△DAP≌△EAP(SAS),
∴PD=PE,
∵FD⊥AC,BC⊥AC,PM⊥AC,
∴FD∥BC∥PM,
∴$\frac{DM}{CM}=\frac{PF}{PB}$,
∵点P是BF的中点,
∴DM=MC,
又∵PM⊥AC,
∴PC=PD,
又∵PD=PE,
∴PC=PE.
(3)如图4,分别取AB、AF的中点N、G,分别连接PN、CN、EG、EC,
证明:由Rt△ACB∽Rt△AEF,
∴等腰△ANC∽等腰△EGA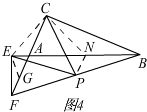
∴$\frac{CN}{CA}=\frac{AG}{AE}$,
∵PN=AG,
∴$\frac{CN}{CA}=\frac{PN}{AE}$,
由N为AB中点易得∠CNB=2∠CAN,且∠PNB=∠GAN
∵∠CAE=360°-2∠CAN-∠GAN
∠CNP=360°-∠CNB-∠PNB
∴∠CAE=∠CNP
∴△CAE∽△CNP(SAS)
∴$\frac{CE}{CP}=\frac{CA}{CN}$,
∴等腰△PCE∽等腰△NCA(SSS)
∴∠CPE=∠CAN
当△CPE总是等边三角形时,∠CPE=∠CAN=60°,所以∠CBA=30°
∴k=$\frac{AC}{BC}=\frac{\sqrt{3}}{3}$.
点评 此题是几何变换综合题,主要考查了直角三角形斜边的中线等于斜边一半,全等三角形的性质和判定,相似三角形的性质和判定,作出辅助线是解本题的关键也是难点.

| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.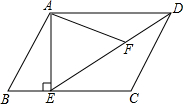 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.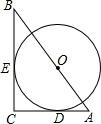 如图,⊙O的圆心在Rt△ABC的斜边AB上,且⊙O分别与边AC、BC相切于D、E两点,已知AC=3,BC=4,则⊙O的半径r=$\frac{12}{7}$.
如图,⊙O的圆心在Rt△ABC的斜边AB上,且⊙O分别与边AC、BC相切于D、E两点,已知AC=3,BC=4,则⊙O的半径r=$\frac{12}{7}$.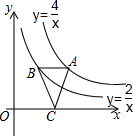 如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.
如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.