题目内容
20.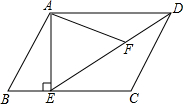 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;
(2)若AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,∠ADE=30°,求AB的长.
分析 (1)由平行四边形的性质得出AD∥BC,AB∥CD,AB=CD,得出∠ADF=∠DEC,∠B+∠C=180°,证出∠AFD=∠C,即可得出结论;
(2)证出AD⊥AE,由∠ADE=30°,求出AE=$\frac{\sqrt{3}}{3}$AD=6,AD=2AE=12,由相似三角形的对应边成比例得出$\frac{AF}{CD}=\frac{AD}{DE}$,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)解:∵AD∥BC,AE⊥BC,
∴AD⊥AE,
∵∠ADE=30°,
∴AE=$\frac{\sqrt{3}}{3}$AD=6,
∴AD=2AE=12,
∵△ADF∽△DEC,
∴$\frac{AF}{CD}=\frac{AD}{DE}$,
即$\frac{4\sqrt{3}}{CD}=\frac{6\sqrt{3}}{12}$,
解得:CD=8,∴AB=8.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质、含30°角的直角三角形的性质;熟练掌握平行四边形的性质、证明三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列计算结果为负数的是( )
| A. | -1+2 | B. | |-1| | C. | $\sqrt{(-2)^{2}}$ | D. | -2-1 |
11.已知A(x1,y1)和B(x2,y2)是函数y=$\frac{{k}^{2}+1}{x}$图象上两点,当x1<x2时,y1与y2之间的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
12. 如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
 如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | C. | $\frac{π}{6}-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{π}{6}-\frac{{\sqrt{3}}}{4}$ |
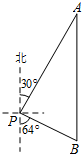 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)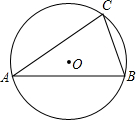 如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.
如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.
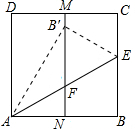 如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.
如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm. 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.