Question

10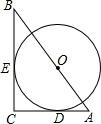．如图，⊙O的圆心在Rt△ABC的斜边AB上，且⊙O分别与边AC、BC相切于D、E两点，已知AC=3，BC=4，则⊙O的半径r=$\frac{12}{7}$．

Answer 1

分析 连结OD、OE，如图，根据切线的性质得∠ODC=∠OEC=90°，再证明四边形OECD为正方形得到CE=r，然后证明△BOE∽△BAC，利用相似比得到r：3=（4-r）：4，再利用比例性质求r即可．

解答 解：连结OD、OE，如图，
∵⊙O分别与边AC、BC相切于D、E两点，
∴OD⊥AC，OE⊥BC，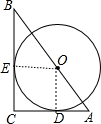
∴∠ODC=∠OEC=90°，
而∠C=90°，
∴四边形OECD为矩形，
而OE=OD，
∴四边形OECD为正方形，
∴CE=r，
∴BE=BC-CE=4-r，
∵OE∥AC，
∴△BOE∽△BAC，
∴OE：AC=BE：BC，即r：3=（4-r）：4，
∴r=$\frac{12}{7}$．
故答案为$\frac{12}{7}$．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．解决本题的关键是证明CE=r．