题目内容
2.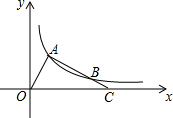 已知△OAC中,∠OAC=90°,OA=2,∠AOC=60°,以O为原点,OC所在直线为x轴建立平面直角坐标系,如图,双曲线y=$\frac{k}{x}$(x>0)的图象经过直角顶点A,并与直角边AC交于点B,则B点的坐标为(3,$\frac{\sqrt{3}}{3}$).
已知△OAC中,∠OAC=90°,OA=2,∠AOC=60°,以O为原点,OC所在直线为x轴建立平面直角坐标系,如图,双曲线y=$\frac{k}{x}$(x>0)的图象经过直角顶点A,并与直角边AC交于点B,则B点的坐标为(3,$\frac{\sqrt{3}}{3}$).
分析 作AE⊥OC,BF⊥OC,易证得△BFC∽△AEC,得出$\frac{BF}{AE}$=$\frac{FC}{EC}$,解直角三角形求得OE=1,AE=$\sqrt{3}$,OC=4,即可求得A的坐标,从而求得反比例函数的解析式,设B(m,$\frac{\sqrt{3}}{m}$),表示出BF=$\frac{\sqrt{3}}{m}$,FC=4-m,EC=3,得到$\frac{\frac{\sqrt{3}}{m}}{\sqrt{3}}$=$\frac{4-m}{3}$,解方程即可求得m的值,进而得出B的坐标.
解答 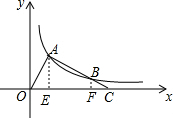 解:作AE⊥OC,BF⊥OC,
解:作AE⊥OC,BF⊥OC,
∴AE∥BF,
∴△BFC∽△AEC,
∴$\frac{BF}{AE}$=$\frac{FC}{EC}$,
∵△OAC中,∠OAC=90°,OA=2,∠AOC=60°,
∴OE=1,AE=$\sqrt{3}$,OC=4,
∴A(1,$\sqrt{3}$),
∴k=1×$\sqrt{3}$=$\sqrt{3}$,
∴y=$\frac{\sqrt{3}}{x}$,
设B(m,$\frac{\sqrt{3}}{m}$),
∴OF=m,BF=$\frac{\sqrt{3}}{m}$,
∴FC=4-m,EC=4-1=3,
∴$\frac{\frac{\sqrt{3}}{m}}{\sqrt{3}}$=$\frac{4-m}{3}$,
解得m=1或m=3,
∴B(3,$\frac{\sqrt{3}}{3}$).
故答案为(3,$\frac{\sqrt{3}}{3}$).
点评 本题考查了反比例函数和一次函数的交点问题,解直角三角形以及三角形相似的判定和性质,解直角三角形求得A的坐标是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.计算(x2)3÷(-x)2的结果是( )
| A. | x2 | B. | x3 | C. | -x3 | D. | x4 |
11.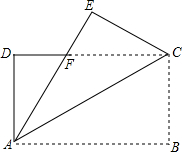 如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )
如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )
 如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )
如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )| A. | 16cm | B. | 20cm | C. | 24cm | D. | 28cm |
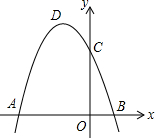 如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3).
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3).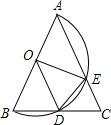 如图,△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E.
如图,△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E.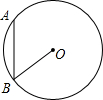 如图,AB是⊙O的弦,AB=6,OB=5,将线段AB向右侧平移,使之与圆相切,点B移至切点位置,则平移的距离为3$\sqrt{10}$.
如图,AB是⊙O的弦,AB=6,OB=5,将线段AB向右侧平移,使之与圆相切,点B移至切点位置,则平移的距离为3$\sqrt{10}$.