题目内容
11.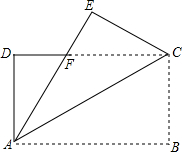 如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )
如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )| A. | 16cm | B. | 20cm | C. | 24cm | D. | 28cm |
分析 首先根据平行线的性质以及折叠的性质证明∠EAC=∠DCA,根据等角对等边证明FC=AF,则DF即可求得,然后在直角△ADF中利用勾股定理求解.
解答 解:∵长方形ABCD中,AB∥CD,
∴∠BAC=∠DCA,
又∵∠BAC=∠EAC,
∴∠EAC=∠DCA,
∴FC=AF=25cm,
又∵长方形ABCD中,DC=AB=32cm,
∴DF=DC-FC=32-25=7cm,
在直角△ADF中,AD=$\sqrt{A{F}^{2}-D{F}^{2}}$=$\sqrt{2{5}^{2}-{7}^{2}}$=24(cm).
故选C.
点评 本题考查了折叠的性质以及勾股定理,在折叠的过程中注意到相等的角以及相等的线段是关键.

练习册系列答案
相关题目
16.若m=$\sqrt{40}$-5,则估计m的值所在的范围是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
3.下列几何体中,主视图是圆的是( )
| A. |  圆柱 | B. |  圆锥 | C. |  球 | D. |  立方体 |
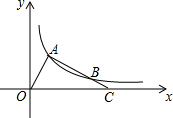 已知△OAC中,∠OAC=90°,OA=2,∠AOC=60°,以O为原点,OC所在直线为x轴建立平面直角坐标系,如图,双曲线y=$\frac{k}{x}$(x>0)的图象经过直角顶点A,并与直角边AC交于点B,则B点的坐标为(3,$\frac{\sqrt{3}}{3}$).
已知△OAC中,∠OAC=90°,OA=2,∠AOC=60°,以O为原点,OC所在直线为x轴建立平面直角坐标系,如图,双曲线y=$\frac{k}{x}$(x>0)的图象经过直角顶点A,并与直角边AC交于点B,则B点的坐标为(3,$\frac{\sqrt{3}}{3}$).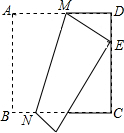 如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,若MN的长为13cm,则CE的长为7cm.
如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,若MN的长为13cm,则CE的长为7cm. 如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积$\frac{7\sqrt{3}}{2}$.
如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积$\frac{7\sqrt{3}}{2}$.
 按要求作图.
按要求作图.