题目内容
13.小明用下面的方法求出方程2$\sqrt{x}$-3=0的解,请你仿照他的方法求出下面两外两个方程的解,并把你的解答过程填写在下面的表格中.| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}>0$ | $\sqrt{x}$=$\frac{3}{2}$,所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则t2+2t-3=0 | t=-3或t=1 | t=-3<0,t=1>0 | $\sqrt{x}$=1,所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t,则t2+t-2=0 | t=-2或t=1 | t=-2<0,t=1>0 | $\sqrt{x-2}$=1,所以x=3 |
分析 令$\sqrt{x}$=t,则t2+2t-3=0,求出t的值,再进行检验;令$\sqrt{x-2}$=t,则t2+t-2=0,求出t的值,再进行检验,最后求出x的值即可.
解答 解:②设$\sqrt{x}$=t(t≥0).则方程即可变形为t2+2t-3=0,
∴(t+3)(t-1)=0,
∴t+3=0或t-1=0,
解得,t=-3(不合题意,舍去),或t=1;
∴$\sqrt{x}$=1,
∴x=1;
③设$\sqrt{x-2}$=t.则方程即可变形为t2+t-2=0,
∴(t+2)(t-1)=0,
∴t+2=0或t-1=0,
解得,t=-2(不合题意,舍去),或t=1;
∴$\sqrt{x-2}$=1,
∴x=3;
故答案为:令$\sqrt{x}$=t,则t2+2t-3=0、t=-3或t=1、t=-3<0,t=1>0、$\sqrt{x}$=1,所以x=1;
令$\sqrt{x-2}$=t,则t2+t-2=0、t=-2或t=1、t=-2<0,t=1>0、$\sqrt{x-2}$=1,所以x=3.
点评 本题考查了解无理方程和解有理方程,关键是能把无理方程转化成有理方程,注意:解无理方程一定要进行检验.

练习册系列答案
相关题目
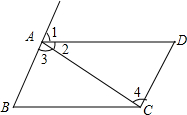 如图,由下列条件可以判定图中哪两条直线平行,说明理由
如图,由下列条件可以判定图中哪两条直线平行,说明理由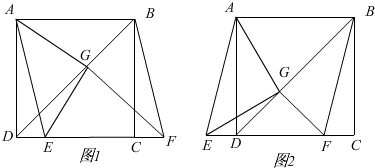
 已知:如图?ABCD中,DM=BN,BE=DF,求证:四边形MENF是平行四边形.
已知:如图?ABCD中,DM=BN,BE=DF,求证:四边形MENF是平行四边形. 如图,PA和PB是⊙O的切线,点A和点B是切点,若OA=9,∠P=40°,则$\widehat{AB}$的长为,7π(结果保留π).
如图,PA和PB是⊙O的切线,点A和点B是切点,若OA=9,∠P=40°,则$\widehat{AB}$的长为,7π(结果保留π).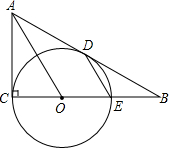 如图,在△ABC中,∠C=90°,点O在CB上,⊙O经过点C,且与AB相切于点D,与CB的另一个交点为E.
如图,在△ABC中,∠C=90°,点O在CB上,⊙O经过点C,且与AB相切于点D,与CB的另一个交点为E.