题目内容
5．
如图，PA和PB是⊙O的切线，点A和点B是切点，若OA=9，∠P=40°，则$\widehat{AB}$的长为，7π（结果保留π）．
分析 根据切线的性质得出∠PAO=∠PBO=90°，求出∠AOB=140°，根据弧长公式求出即可．
解答 解：∵PA和PB是⊙O的切线，点A和点B是切点，
∴∠PAO=∠PBO=90°，
∵∠P=40°，
∴∠AOB=360°-90°-90°-40°=140°，
∴$\widehat{AB}$的长为$\frac{140π×9}{180}$=7π，
故答案为：7π
点评 本题考查了切线的性质，弧长公式的应用，能根据切线的性质求出∠PAO=∠PBO=90°是解此题的关键，注意：圆的切线垂直于过切点的半径．
练习册系列答案
相关题目
如图，已知∠1=∠2，BD平分∠ABC，可得到那两条直线平行？如果要得到另外两条直线平行，则应将上述两个条件之一做如何改变？
13．小明用下面的方法求出方程2$\sqrt{x}$-3=0的解，请你仿照他的方法求出下面两外两个方程的解，并把你的解答过程填写在下面的表格中．
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t，则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}＞0$ | $\sqrt{x}$=$\frac{3}{2}$，所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t，则t2+2t-3=0 | t=-3或t=1 | t=-3＜0，t=1＞0 | $\sqrt{x}$=1，所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t，则t2+t-2=0 | t=-2或t=1 | t=-2＜0，t=1＞0 | $\sqrt{x-2}$=1，所以x=3 |
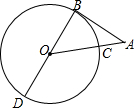如图，BD为⊙O的直径，AB与⊙O相切于点B，连结AO，AO与⊙O交于点C，若∠A=40°，⊙O的半径为2，则$\widehat{CD}$的长为$\frac{13}{9}$π．
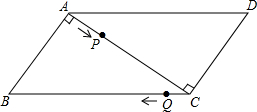已知，如图，用两块一样大的直角三角板拼成一个平行四边形，∠BAC=∠ACD=90°．在?ABCD中，AB=3cm，BC=5cm，点P自A向C、沿AC的方向匀速运动，速度为1cm/s；同时，点Q从点C出发，自C向B、沿CB方向匀速运动，速度为1cm/s；过点P作PM⊥AD，并与AD相交于点M，当P、Q中有一个点到达终点时，另一个点也停止运动．设运动时间为t（s）．解答下列问题：
15．自成都地铁4号线开通以来，成都地铁1、2、4号线线网客流增加明显，再遇到春季糖酒会、桃花节、通勤客流等三股主要客流汇集，2016年3月25日，成都地铁再创单日线网客流历史新高，达到1738200乘次，用科学记数法表示1738200为（保留三个有效数字）（ ）
| A． | 1.74×106 | B． | 1.73×106 | C． | 17.4×105 | D． | 17.3×105 |