题目内容
3.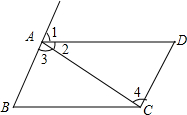 如图,由下列条件可以判定图中哪两条直线平行,说明理由
如图,由下列条件可以判定图中哪两条直线平行,说明理由(1)若∠1=∠B,则AD∥BC;
(2)若∠3=∠4,则AB∥DC;
(3)若∠1=∠D,则AB∥DC;
(4)若∠2+∠3+∠B=180°,则AD∥BC.
分析 (1)根据同位角相等,两直线平行得出即可;
(2)根据内错角相等,两直线平行得出即可;
(3)根据内错角相等,两直线平行得出即可;
(4)根据同旁内角互补,两直线平行得出即可.
解答 解:(1)∵∠1=∠B,
∴AD∥BC(同位角相等,两直线平行),
故答案为:AD,BC;
(2)∵∠3=∠4(内错角相等,两直线平行),
∴AB∥DC,
故答案为:AB,DC;
(3)∵∠1=∠D,
∴AB∥DC(内错角相等,两直线平行),
故答案为:AB,DC;
(4)∵∠2+∠3+∠B=180°,
∴AD∥BC(同旁内角互补,两直线平行),
故答案为:AD,BC.
点评 本题考查了平行线的判定的应用,能正确运用定理进行推理是解此题的关键,注意:平行线的判定有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行.

练习册系列答案
相关题目
18.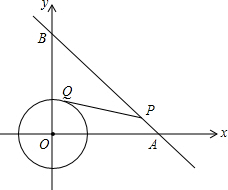 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 6-$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
13.小明用下面的方法求出方程2$\sqrt{x}$-3=0的解,请你仿照他的方法求出下面两外两个方程的解,并把你的解答过程填写在下面的表格中.
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}>0$ | $\sqrt{x}$=$\frac{3}{2}$,所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则t2+2t-3=0 | t=-3或t=1 | t=-3<0,t=1>0 | $\sqrt{x}$=1,所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t,则t2+t-2=0 | t=-2或t=1 | t=-2<0,t=1>0 | $\sqrt{x-2}$=1,所以x=3 |
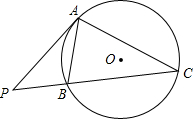 如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线.
如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线.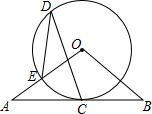 如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F.
如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F. 如图,已知∠1=∠2,BD平分∠ABC,可得到那两条直线平行?如果要得到另外两条直线平行,则应将上述两个条件之一做如何改变?
如图,已知∠1=∠2,BD平分∠ABC,可得到那两条直线平行?如果要得到另外两条直线平行,则应将上述两个条件之一做如何改变?