题目内容
1.关于x的方程(a2-4a+5)x2-2ax+4=0.(1)试证明:无论a取何实数这个方程都是一元二次方程;
(2)若这个方程的两根x1,x2是等腰三角形ABC的两腰,求出整数a的值.
分析 (1)要证明无论a取何实数这个方程都是一元二次方程,只要说明无论a为什么值时a2-4a+5的值都不是0,可以利用配方法来证明;
(2)根据等腰三角形的定义得到x1=x2,于是得到结论.
解答 解:(1)a2-4a+5=(a2-4a+4)+1=(a-2)2+1,
∵(a-2)2≥0,
∴(a-2)2+1≠0,
∴无论a取何实数关于x的方程(a2-4a+5)x2+2ax+4=0都是一元二次方程;
(2)∵这个方程的两根x1,x2是等腰三角形ABC的两腰,
∴x1=x2,
∴(a-2)2=0,
∴a=2.
点评 本题考查的是解一元二次方程,熟知解一元二次方程的因式分解法是解答此题的关键.

练习册系列答案
相关题目
9.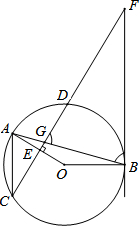 如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是⊙0的切线;
(2)若DG=2,DF=3,求BG的长.
 如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.(1)若∠FGB=∠FBG,求证:BF是⊙0的切线;
(2)若DG=2,DF=3,求BG的长.
13.小明用下面的方法求出方程2$\sqrt{x}$-3=0的解,请你仿照他的方法求出下面两外两个方程的解,并把你的解答过程填写在下面的表格中.
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}>0$ | $\sqrt{x}$=$\frac{3}{2}$,所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则t2+2t-3=0 | t=-3或t=1 | t=-3<0,t=1>0 | $\sqrt{x}$=1,所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t,则t2+t-2=0 | t=-2或t=1 | t=-2<0,t=1>0 | $\sqrt{x-2}$=1,所以x=3 |
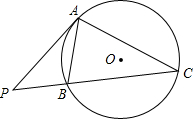 如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线.
如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线. 如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为$\frac{81π}{4}$.
如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为$\frac{81π}{4}$.