题目内容
8．
已知：如图?ABCD中，DM=BN，BE=DF，求证：四边形MENF是平行四边形．
分析 根据SAS可以证明△DMF≌△BNE．从而得到MF=NE，∠DFM=∠BEN．根据等角的补角相等，可以证明∠NEF=∠EFM，则EN∥FM．根据一组对边平行且相等的四边形是平行四边形即可证明．
解答 证明：在平行四边形ABCD中，AD∥BC，
∴∠ADB=∠CBD．
在△BNE和△DMF中，$\left\{\begin{array}{l}{BN=DM}&{\;}\\{∠CBD=∠ADB}&{\;}\\{BE=DF}&{\;}\end{array}\right.$，
∴△BNE≌△DMF（SAS）．
∴MF=NE，∠DFM=∠BEN，
∴∠MFE=∠NEF，
∴EN∥FM．
∴四边形MENF是平行四边形．
点评 此题综合运用了平行四边形的性质和判定、全等三角形的判定与性质．熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．
练习册系列答案
相关题目
18．
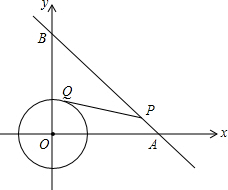如图，⊙O是以原点为圆心，$\sqrt{2}$为半径的圆，点P是直线y=-x+6上的一点，过点P作⊙O的一条切线PQ，Q为切点，则S△PQO的最小值为（ ）
如图，⊙O是以原点为圆心，$\sqrt{2}$为半径的圆，点P是直线y=-x+6上的一点，过点P作⊙O的一条切线PQ，Q为切点，则S△PQO的最小值为（ ）| A． | 3 | B． | 4$\sqrt{2}$ | C． | 6-$\sqrt{2}$ | D． | 2$\sqrt{2}$ |
13．小明用下面的方法求出方程2$\sqrt{x}$-3=0的解，请你仿照他的方法求出下面两外两个方程的解，并把你的解答过程填写在下面的表格中．
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t，则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}＞0$ | $\sqrt{x}$=$\frac{3}{2}$，所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t，则t2+2t-3=0 | t=-3或t=1 | t=-3＜0，t=1＞0 | $\sqrt{x}$=1，所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t，则t2+t-2=0 | t=-2或t=1 | t=-2＜0，t=1＞0 | $\sqrt{x-2}$=1，所以x=3 |
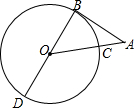如图，BD为⊙O的直径，AB与⊙O相切于点B，连结AO，AO与⊙O交于点C，若∠A=40°，⊙O的半径为2，则$\widehat{CD}$的长为$\frac{13}{9}$π．
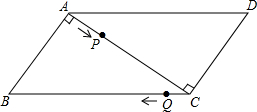已知，如图，用两块一样大的直角三角板拼成一个平行四边形，∠BAC=∠ACD=90°．在?ABCD中，AB=3cm，BC=5cm，点P自A向C、沿AC的方向匀速运动，速度为1cm/s；同时，点Q从点C出发，自C向B、沿CB方向匀速运动，速度为1cm/s；过点P作PM⊥AD，并与AD相交于点M，当P、Q中有一个点到达终点时，另一个点也停止运动．设运动时间为t（s）．解答下列问题：