题目内容
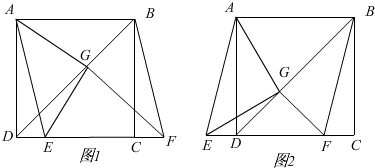
4.在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是AG=EG,位置关系是AG⊥EG;
(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;
(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.
分析 (1)由平移得到EF=AD,再由正方形的性质得出∠ADG=∠CDB,DG=FG,从而证明△AGD≌△EGF即可;
(2)由平移得到EF=AD,再由正方形的性质得出∠ADG=∠CDB,DG=FG,从而证明△AGD≌△EGF即可;
(3)由(1)的结论AG=EG,AG⊥EG,得出∠GEA=45°,推导出∠AED=30°,再由三角函数即可求解.
解答 解:(1)如图1,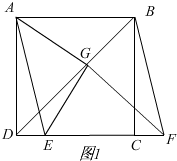
由平移得,EF=AD,
∵BD是正方形的对角线,
∴∠ADB=∠CDB=45°,
∵GF⊥BD,
∴∠DGF=90°,
∴∠GFD+∠CBD=90°,
∴∠DFG=45°,
∴GD=GF,
在△AGD和△EGF中,
$\left\{\begin{array}{l}{AD=EF}\\{∠ADG=∠EFG}\\{DG=FG}\end{array}\right.$,
∴△AGD≌△EGF
∴AG=EG,∠AGD=∠EGF,
∴∠AGE=∠AGD+∠DGE=∠EGF+DGE=90°,
∴AG⊥EG.
故答案为AG=EG,AG⊥EG.
(2)(1)中的结论仍然成立,
证明:如图2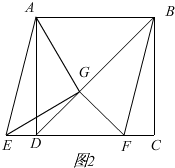
由平移得,EF=AD,
∵BD是正方形的对角线,
∴∠ADB=∠CDB=45°,
∵GF⊥BD,
∴∠DGF=90°,
∴∠GFD+∠CBD=90°,
∴∠DFG=45°,
∴GD=GF,
在△AGD和△EGF中,
$\left\{\begin{array}{l}{AD=EF}\\{∠ADG=∠EFG}\\{DG=FG}\end{array}\right.$,
∴△AGD≌△EGF
∴AG=EG,∠AGD=∠EGF,
∴∠AGE=∠AGD-∠DGE=∠EGF-∠DGE=90°,
∴AG⊥EG.
(3)如图3,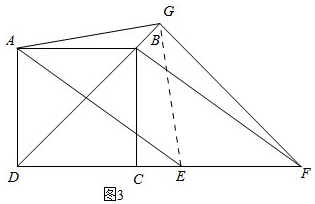 连接EG,
连接EG,
由(1)有,AG=EG,AG⊥EG,
∴∠GEA=45°,
∵∠AGF=120°,∠DGF=90°,
∴∠AGB=∠FGE=30°,∠DGE=60°,
∴∠DEG=75°,
∵GD=GF,
∴∠GDF=∠GFD=45°,
∴∠AED=30°,
在Rt△ADE中,AD=2,
∴DE=2$\sqrt{3}$.
点评 此题是四边形综合题,主要考查了全等三角形的判定和性质,平移的性质,找出△AGD≌△EGF的条件是解本题的关键.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案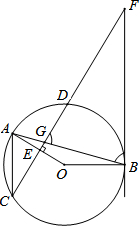 如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.(1)若∠FGB=∠FBG,求证:BF是⊙0的切线;
(2)若DG=2,DF=3,求BG的长.
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}>0$ | $\sqrt{x}$=$\frac{3}{2}$,所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则t2+2t-3=0 | t=-3或t=1 | t=-3<0,t=1>0 | $\sqrt{x}$=1,所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t,则t2+t-2=0 | t=-2或t=1 | t=-2<0,t=1>0 | $\sqrt{x-2}$=1,所以x=3 |
 如图,已知∠1=∠2,BD平分∠ABC,可得到那两条直线平行?如果要得到另外两条直线平行,则应将上述两个条件之一做如何改变?
如图,已知∠1=∠2,BD平分∠ABC,可得到那两条直线平行?如果要得到另外两条直线平行,则应将上述两个条件之一做如何改变?