题目内容
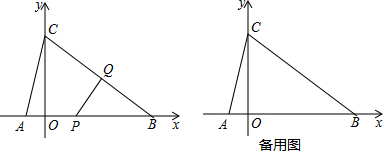
9. 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )| A. | 115° | B. | 120° | C. | 125° | D. | 130° |
分析 根据圆周角定理和圆内接四边形的性质即可得到结论.
解答 解:如图,在优弧AB上取一点D,连接AD,BD,
则∠ADB=$\frac{1}{2}$AOB=65°,
∴∠ACB=180°-∠ADB=115°.
故选A.
点评 本题考查了圆周角定理、圆内接四边形的性质,熟练掌握圆周角定理是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
20.关于x的一元二次方程mx2+2x+1=0有两个不相等的实数根,则m的取值范围是( )
| A. | m<1 | B. | m≤1 | C. | m<1且m≠0 | D. | m≤1且m≠0 |
4.已知一组数据:1,2,6,3,3,下列说法错误的是( )
| A. | 众数是3 | B. | 中位数是6 | C. | 平均数是3 | D. | 方差是2.8 |
14. 如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
 如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
18.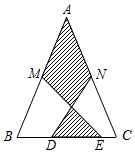 如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
 如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.| A. | 25 | B. | 35 | C. | 30 | D. | 42 |
19.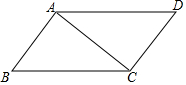 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
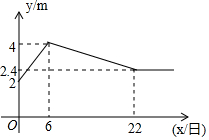 如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.
如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.