题目内容
19.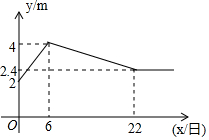 如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.
如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
分析 观察函数图象找出点的坐标,利用待定系数法求出y与x之间的函数关系式,代入y=3求出x的值,由此即可得出结论.
解答 解:设y与x之间的函数关系式为y=kx+b,
当0≤x≤6时,将(0,2)、(6,4)代入y=kx+b中,
$\left\{\begin{array}{l}{b=2}\\{6k+b=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=2}\end{array}\right.$,
∴y=$\frac{1}{3}$x+2(0≤x≤6);
当6≤x≤22时,将(6,4)、(22,2.4)代入y=kx+b中,
$\left\{\begin{array}{l}{6k+b=4}\\{22k+b=2.4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-0.1}\\{b=4.6}\end{array}\right.$,
∴y=-0.1x+4.6;
当x≥22时,y=2.4.
令y=$\frac{1}{3}$x+2=3,解得:x=3;
令y=-0.1x+4.6=3,解得x=16.
16-3+1=14.
故选D.
点评 本题考查了函数图象、待定系数法求出一次函数解析式以及一次函数图象上点的坐标,观察函数图象找出点的坐标,利用待定系数法求出y与x之间的函数关系式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.若点(-2,y1)、(-1,y2)在反比例函数y=-$\frac{6}{x}$的图象上,则下列结论正确的是( )
| A. | y1>y2>0 | B. | y2>y1>0 | C. | 0>y1>y2 | D. | 0>y2>y1 |
9. 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )| A. | 115° | B. | 120° | C. | 125° | D. | 130° |
 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.