题目内容
18.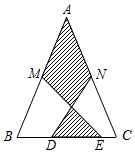 如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.| A. | 25 | B. | 35 | C. | 30 | D. | 42 |
分析 连接MN,根据中位线定理,可得出MN=DE=5cm;图中阴影部分的面积就是图中三个三角形的面积,由图可知,这三个三角形的底相等都是5cm,这三个三角形的高之和是从A点到BC的垂线段的长,利用勾股定理可求得高的值,据此可求出图中阴影部分的面积.
解答 解: 连接MN,过点A作AF⊥BC于F,
连接MN,过点A作AF⊥BC于F,
则MN是△ABC的中位线,
因此MN=$\frac{1}{2}$BC=5cm;
则AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=12cm.
∵图中阴影部分的三个三角形的底长都是5cm,且高的和为12cm;
因此S阴影=$\frac{1}{2}$×5×12=30cm2.
故选:C.
点评 本题主要考查了中位线定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
9. 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )| A. | 115° | B. | 120° | C. | 125° | D. | 130° |
6.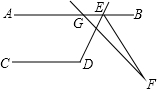 如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
 如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )| A. | 24° | B. | 12° | C. | 11° | D. | 10° |
13.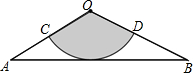 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )| A. | 10 cm | B. | 15 cm | C. | 10$\sqrt{3}$ cm | D. | 20$\sqrt{2}$ cm |
3.函数y=$\sqrt{2x-4}$中自变量x的取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≤2 | D. | x≠2 |
10. 如图,下列条件中,能判定a∥b的是( )
如图,下列条件中,能判定a∥b的是( )
 如图,下列条件中,能判定a∥b的是( )
如图,下列条件中,能判定a∥b的是( )| A. | ∠1=∠2 | B. | ∠1=∠4 | C. | ∠1+∠3=180° | D. | ∠3+∠4=180° |