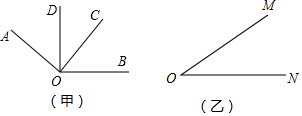题目内容
19.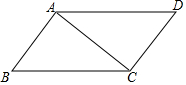 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 证出△ACD是等腰直角三角形,由勾股定理求出AD,即可得出BC的长.
解答 解:∵四边形ABCD是平行四边形,
∴CD=AB=2,BC=AD,∠D=∠ABC=∠CAD=45°,
∴AC=CD=2,∠ACD=90°,
即△ACD是等腰直角三角形,
∴BC=AD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
故选:C.
点评 本题考查了平行四边形的性质、勾股定理、等腰直角三角形的判定与性质;熟练掌握平行四边形的性质,证明△ACD是等腰直角三角形是解决问题的关键.

练习册系列答案
相关题目
9. 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )| A. | 115° | B. | 120° | C. | 125° | D. | 130° |
10. 如图,下列条件中,能判定a∥b的是( )
如图,下列条件中,能判定a∥b的是( )
 如图,下列条件中,能判定a∥b的是( )
如图,下列条件中,能判定a∥b的是( )| A. | ∠1=∠2 | B. | ∠1=∠4 | C. | ∠1+∠3=180° | D. | ∠3+∠4=180° |
14.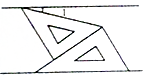 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )| A. | 15° | B. | 22.5° | C. | 30° | D. | 45° |
4.丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
| v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
| t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
 如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=20°.
如图,已知l1∥l2,直线l与l1、l2相交于C、D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=20°.