题目内容
14. 如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,由对称的性质可知$\widehat{AN}$=$\widehat{A'N}$,再由圆周角定理可求出∠A′ON的度数,再由勾股定理即可求解.
解答 解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,
连接OB,OA′,AA′,
∵AA′关于直线MN对称,
∴$\widehat{AN}$=$\widehat{A'N}$,
∵∠AMN=40°,
∴∠A′ON=80°,∠BON=40°,
∴∠A′OB=120°,
过O作OQ⊥A′B于Q,
在Rt△A′OQ中,OA′=4,
∴A′B=2A′Q=4$\sqrt{3}$,
即PA+PB的最小值4$\sqrt{3}$.
故选D.
点评 本题考查的是轴对称-最短路线问题,圆周角定理及勾股定理,解答此题的关键是根据题意作出辅助线,构造出直角三角形,利用勾股定理求解.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
4.若点(-2,y1)、(-1,y2)在反比例函数y=-$\frac{6}{x}$的图象上,则下列结论正确的是( )
| A. | y1>y2>0 | B. | y2>y1>0 | C. | 0>y1>y2 | D. | 0>y2>y1 |
5. 如图,函数y=-2x2 的图象是( )
如图,函数y=-2x2 的图象是( )
 如图,函数y=-2x2 的图象是( )
如图,函数y=-2x2 的图象是( )| A. | ① | B. | ② | C. | ③ | D. | ④ |
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9. 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
 如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=130°,则∠ACB的度数是( )| A. | 115° | B. | 120° | C. | 125° | D. | 130° |
19.数轴上的两个数-3与a,并且a>-3,它们之间的距离可以表示为( )
| A. | 3-a | B. | -3-a | C. | a-3 | D. | a+3 |
6.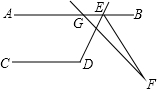 如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
 如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )| A. | 24° | B. | 12° | C. | 11° | D. | 10° |
3.函数y=$\sqrt{2x-4}$中自变量x的取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≤2 | D. | x≠2 |
4.丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
| v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
| t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.