题目内容
13.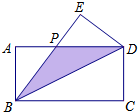 如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.(1)BD=$\sqrt{20}$(或$2\sqrt{5}$);
(2)点P到BD的距离是$\frac{5}{{\sqrt{20}}}$(或$\frac{{\sqrt{5}}}{2}$).
分析 (1)由勾股定理直接得出;
(2)设AP=x,证出△ABP≌△EDP,可知EP=x,PD=8-x,根据翻折不变性,可知ED=DC=AB=2,然后在Rt△PED中,利用勾股定理求出x,再由三角形的面积即可求出结论.
解答 解:(1)∵四边形ABCD是长方形,
∴∠C=90°,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
故答案为2$\sqrt{5}$;
(2)在△APB与△DEP中,
$\left\{\begin{array}{l}{∠APB=∠EPD}\\{∠A=∠E=90°}\\{AB=ED}\end{array}\right.$,
∴△APB≌△DEP,
∴AP=EP,
设AP=x,可知EP=x,PD=4-x,
∴在Rt△PED中,
x2+22=(4-x)2,
解得x=$\frac{3}{2}$.
即AP=$\frac{3}{2}$,
∴PD=4-$\frac{3}{2}$=$\frac{5}{2}$,
∴△BDP的面积=$\frac{1}{2}$×$\frac{5}{2}$×2=$\frac{1}{2}$×2$\sqrt{5}$•点P到BD的距离,
∴点P到BD的距离=$\frac{\sqrt{5}}{2}$,
故答案为$\frac{\sqrt{5}}{2}$.
点评 本题主要考查的是翻折的性质、平行线的性质、等腰三角形的判定、勾股定理的应用,在△ADP中利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
3.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三内角之比为3:4:5 | B. | 三边之比为1:1:$\sqrt{2}$ | ||
| C. | 三边长分别为5、13、12 | D. | 有两锐角分别为32°、58° |
4.下列根式中属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{27}$ |
8.下列说法中,正确的是( )
| A. | $\sqrt{16}$等于±4 | B. | -42的平方根是±4 | C. | 8的立方根是±2 | D. | -$\sqrt{5}$是5的平方根 |
 已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上
已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上