题目内容
18.如图,顶点为($\frac{1}{2}$,$\frac{9}{4}$)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,2),与x轴交于A、B两点.(1)求抛物线解析式及A、B两点坐标;
(2)在抛物线对称轴上有一点P,使P到A、C两点的距离和最短,求点P坐标;
(3)若点Q为x轴上任意一点,在抛物线上是否存在点R,使以A、C、Q、R为顶点的四边形是平行四边形?若存在,直接写出R点坐标;若不存在,请说明理由.
分析 (1)由顶点为($\frac{1}{2}$,$\frac{9}{4}$)的抛物线y=ax2+bx+c(a≠0),可设抛物线解析式为:y=a(x-$\frac{1}{2}$)2+$\frac{9}{4}$,然后由点C(0,2),求得抛物线的解析式;继而求得A、B两点坐标;
(2)易得连接BC交对称轴与点P,就是到A、C两点的距离和最短的P点,然后求得直线BC的解析式,继而求得答案;
(3)分别从当CR∥AQ与AC∥QR,去分析求解即可求得答案.
解答 解:(1)设抛物线解析式为:y=a(x-h)2+k,
∵抛物线顶点为($\frac{1}{2}$,$\frac{9}{4}$),
∴抛物线解析式为:y=a(x-$\frac{1}{2}$)2+$\frac{9}{4}$,
∵抛物线与y轴交于点C(0,2)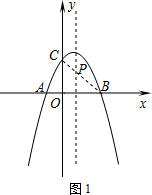 ∴2=a(0-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴2=a(0-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴a=-1
∴y=-(x-$\frac{1}{2}$)2+$\frac{9}{4}$=-x2+x+2;
当y=0时,即:-x2+x+2=0,
解得:x1=-1,x2=2,
∴A(-1,0),B (2,0);
(2)∵抛物线顶点为($\frac{1}{2}$,$\frac{9}{4}$)
∴对称轴是直线x=$\frac{1}{2}$,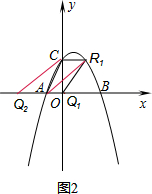 ∵点A、B关于对称轴x=$\frac{1}{2}$对称,
∵点A、B关于对称轴x=$\frac{1}{2}$对称,
∴连接BC交对称轴与点P,就是到A、C两点的距离和最短的P点,
设直线BC解析式为y=kx+b,
∴$\left\{\begin{array}{l}{0=2k+b}\\{2=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
∴y=-x+2,
当x=$\frac{1}{2}$时,y=$\frac{3}{2}$,
∴点P坐标为($\frac{1}{2}$,$\frac{3}{2}$);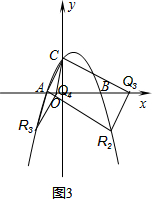
(3)如图2,当CR∥AQ时,R1的坐标为(1,2);
如图3,若AC∥QR,则R的纵坐标为:-2,
∴-x2+x+2=-2,
解得:x=$\frac{1±\sqrt{17}}{2}$,
∴R2的坐标为($\frac{1+\sqrt{17}}{2}$,-2);R3的坐标为($\frac{1-\sqrt{17}}{2}$,-2);
综上所述:R点坐标为:(1,2),($\frac{1+\sqrt{17}}{2}$,-2),($\frac{1-\sqrt{17}}{2}$,-2).
点评 此题属于二次函数的综合题,考查了待定系数求函数解析式、线段和最短问题以及平行四边形的性质.注意根据题意画出图形,结合图形求解是关键.

| A. | 它的准确值x的范围是0.70475<x<0.70485 | |
| B. | 它有三个有效数字 | |
| C. | 对它四舍五入精确到百分位为0.71 | |
| D. | 用科学记数法表示它为7.048×10-1 |
| A. | 6.5cm | B. | 7cm | C. | 7.5cm | D. | 8cm |
 如图,在菱形ABCD中,sin∠D=$\frac{4}{5}$,E,F分别是AB和CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC是直角三角形时,CP的长为$\sqrt{5}$或4或$\frac{20}{11}$.
如图,在菱形ABCD中,sin∠D=$\frac{4}{5}$,E,F分别是AB和CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC是直角三角形时,CP的长为$\sqrt{5}$或4或$\frac{20}{11}$.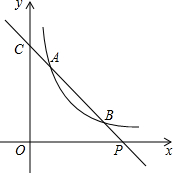 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C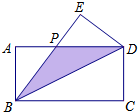 如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
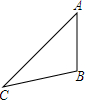 如图,△ABC中,∠B=100°,按要求完成画图并解答问题:
如图,△ABC中,∠B=100°,按要求完成画图并解答问题: