题目内容
1.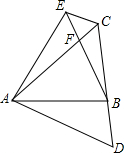 已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上
已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上(1)求证:CE=BD;
(2)求证:∠AFE=∠ABD;
(3)若AC=2,求△ECB的周长最小值.
分析 (1)根据全等三角形的性质即可得到结论;
(2)根据三角形的内角和得到∠AFE=120°-∠1,∠ABD═120°-∠3,由于∠1=∠3,于是得到∠AFE=∠ABD;
(3)根据等边三角形的性质得到EB=AB,由于CE=BD,于是得到△ECB的周长=EB+BC+EC=AB+BC+BD=AB+CD=AB+AC=AB+2,当AB最小时,△ECB的周长最小,当AB⊥CD时,AB最小,即可得到结论.
解答 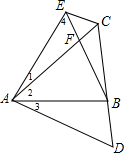 (1)证明:在△AEC与△ABD中,
(1)证明:在△AEC与△ABD中,
$\left\{\begin{array}{l}{AC=AD}\\{∠1=∠3}\\{AE=AB}\end{array}\right.$,
∴△AEC≌△ABD,
∴CE=BD;
(2)证明:∵∠AFE=180°-∠1-∠4=180°-∠1-60°=120°-∠1,
∠ABD=180°-∠3-∠D=180°-∠3-60°=120°-∠3,
∵∠1=∠3,
∴∠AFE=∠ABD;
(3)解:∵△AEB是等边三角形,
∴EB=AB,
∵CE=BD,
∴△ECB的周长=EB+BC+EC=AB+BC+BD=AB+CD=AB+AC=AB+2,
∴当AB最小时,△ECB的周长最小,
当AB⊥CD时,AB最小,
∴AB=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴ECB的周长最小值=2+$\sqrt{3}$.
点评 本题考查的是图形旋转的性质及等边三角形的判定与性质,熟知旋转前、后的图形全等是解答此题的关键.

练习册系列答案
相关题目
11.下列计算中正确的是( )
| A. | a2•a4=a8 | B. | a5•a5=2a10 | C. | b2+b2=b4 | D. | a10•a=a11 |
12.计算2$\sqrt{2}$-$\sqrt{2}$正确的是( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 3$\sqrt{2}$ |
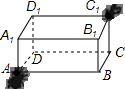 如图,有一长为6cm,宽为5cm,高为3cm的长方体,在它的底面A点有一只蚂蚁.
如图,有一长为6cm,宽为5cm,高为3cm的长方体,在它的底面A点有一只蚂蚁.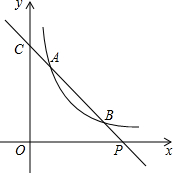 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C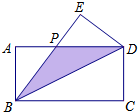 如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.