题目内容
3.某公园要建造一个圆形喷水池,在水池中央垂直于水面竖一根柱子,连喷头在内柱高为1m,水流在各个方向上沿形状相同的抛物线形路径落下,如图①所示,已知在图②中,抛物线的最高点M距离柱子OA为1m,距离地面OB为2m.(1)求图②中抛物线的函数表达式(不必求x的取值范围).
(2)如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内(精确到0.01m)?
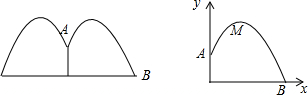
分析 (1)根据题意可设解析式为顶点式形式,由A(0,1)、M(1,2)两点坐标求解析式;
(2)求水池半径即时求当y=0时x的值.
解答 解:(1)设这条抛物线解析式为y=a(x-h)2+k
由题意知:顶点M为(1,2),A为(0,1)
∴k=2,1=a(0-1)2+2,
解得:a=-1.
所以这条抛物线的解析式为y=-(x-1)2+2.
(2)令y=0,则0=-(x-1)2+2,
解得x1≈2.41,x2≈-0.41(舍).
答:若不计其它因素,水池的半径至少2.41米,才能使喷出的水流不至于落在池外.
点评 本题考查二次函数的实际应用,根据实际问题求二次函数,再运用二次函数求最大值.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
14.若x+y=m,xy=-3,则化简(x-3)(y-3)的结果是( )
| A. | 12 | B. | 3m+6 | C. | -3m-12 | D. | -3m+6 |
18.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 矩形 | D. | 正五边形 |
9.下列给出的式子一定是二次根式的是( )
| A. | $\sqrt{{a}^{2}-2}$ | B. | $\sqrt{{x}^{2}+2}$ | C. | $\sqrt{3-π}$ | D. | $\root{3}{a}$ |
10.若-2a<-2b,则a>b,则根据是( )
| A. | 不等式的基本性质1 | B. | 不等式的基本性质2 | ||
| C. | 不等式的基本性质3 | D. | 等式的基本性质2 |
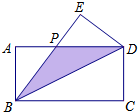 如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.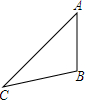 如图,△ABC中,∠B=100°,按要求完成画图并解答问题:
如图,△ABC中,∠B=100°,按要求完成画图并解答问题: