题目内容
5.已知关于x的一元二次方程x2-2(m+2)x+m2+1=0,有两实数根.(1)求m的取值范围;
(2)设方程两根分别为x1,x2,且满足|x1|+|x2|=|x1x2|-5,求m的值.
分析 (1)由根的判别式列出不等式,解不等式可得m的取值范围;
(2)由韦达定理可得x1+x2=2m+4、x1x2=m2+1,结合m的范围可判断x1>0、x2>0,继而化简|x1|+|x2|=|x1x2|-5,代入可得关于m的一元二次方程,解方程根据m的范围取舍可得.
解答 解:(1)根据题意,△=4(m+2)2-4(m2+1)≥0,即16m+12≥0,
解得:m≥-$\frac{3}{4}$;
(2)由韦达定理知,x1+x2=2(m+2)=2m+4,x1x2=m2+1,
∵m≥-$\frac{3}{4}$,
∴x1+x2=2m+4≥$\frac{5}{2}$>0,x1x2=m2+1>0,
∴x1>0,x2>0,
则|x1|+|x2|=|x1x2|-5可化为x1+x2=x1x2-5,
即2m+4=m2+1-5,
整理,得:m2-2m-8=0,
解得:m=-2或m=4,
∵m=-2<-$\frac{3}{4}$,舍去,
∴m=4.
点评 本题主要考查一元二次方程根的判别式、根与系数的关系,根据m的范围和根与系数的关系判断两根均为正数是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
14.若x+y=m,xy=-3,则化简(x-3)(y-3)的结果是( )
| A. | 12 | B. | 3m+6 | C. | -3m-12 | D. | -3m+6 |
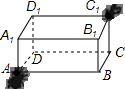 如图,有一长为6cm,宽为5cm,高为3cm的长方体,在它的底面A点有一只蚂蚁.
如图,有一长为6cm,宽为5cm,高为3cm的长方体,在它的底面A点有一只蚂蚁.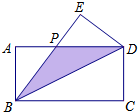 如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4. 如图,将?ABCD沿EF折叠,点A与点C重合,点D落在点C处,若AB=6,BC=4,∠B=60°,则△CEF的面积为$\frac{7\sqrt{3}}{2}$.
如图,将?ABCD沿EF折叠,点A与点C重合,点D落在点C处,若AB=6,BC=4,∠B=60°,则△CEF的面积为$\frac{7\sqrt{3}}{2}$.