题目内容
15.先化简,再求值:($\frac{1}{a}$-$\frac{1}{b}$)÷$\frac{{a}^{2}-{b}^{2}}{ab}$,其中a=$\sqrt{2}$+1,b=$\sqrt{2}$-1.分析 先算括号里面的,再算除法,分式化为最简后把a、b的值代入进行计算即可.
解答 解:原式=($\frac{b-a}{ab}$)•$\frac{ab}{(a+b)(a-b)}$
=-$\frac{1}{a+b}$.
当a=$\sqrt{2}$+1,b=$\sqrt{2}$-1时,
原式=-$\frac{1}{(\sqrt{2}+1)+(\sqrt{2}-1)}$=-$\frac{1}{2\sqrt{2}}$=-$\frac{\sqrt{2}}{4}$.
点评 本题考查的是分式的化简求值,化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.

练习册系列答案
相关题目
3.石家庄地铁工程于2012年9月28如正式开工建设,到2020年将建成轨道交通1、2、3号线一期工程,其中1号线一期工程轨道全长约23900m,用科学记数法表示1号线一期工程的轨道全长是( )
| A. | 0.239×105m | B. | 2.39×105m | C. | 2.39×104m | D. | 23.9×103m |
10.某班5名同学在一次“1分钟仰卧起坐”测试中,成绩为(单位:次):38,44,42,38,39.这组数据的众数是( )
| A. | 40.2 | B. | 40 | C. | 39 | D. | 38 |
14.完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完全这件事的不同办法数是各类不同方法种树的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分别几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分布计数原理,也叫做乘法原理.
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
小王想获得至少30分的加分,那么概率为多少?
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
| 加分 | 人数 |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
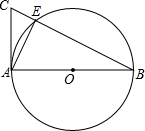 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于E点,若$\frac{OA}{CE}=\sqrt{5}$,则$\frac{AE}{AB}$=$\frac{\sqrt{5}}{5}$.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于E点,若$\frac{OA}{CE}=\sqrt{5}$,则$\frac{AE}{AB}$=$\frac{\sqrt{5}}{5}$. 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点C为圆心,OA的长为直径作半圆交OE于点D.若OA=4,则图中阴影部分的面积为$\frac{5π}{3}$-2$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点C为圆心,OA的长为直径作半圆交OE于点D.若OA=4,则图中阴影部分的面积为$\frac{5π}{3}$-2$\sqrt{3}$.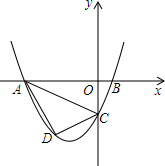 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.