题目内容
6.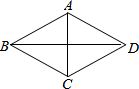 如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )
如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )| A. | 5 | B. | 10 | C. | 5$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
分析 由四边形ABCD是菱形,根据菱形的性质可得∠ACB=$\frac{1}{2}$BCD=$\frac{1}{2}$×120°=60°,AC⊥BD,OC=$\frac{1}{2}$AC=$\frac{1}{2}$×5=2.5,BD=2OB,又由三角函数的性质,即可求得答案.
解答 解:∵四边形ABCD是菱形,
∴∠ACB=$\frac{1}{2}$BCD=$\frac{1}{2}$×120°=60°,AC⊥BD,OC=$\frac{1}{2}$AC=$\frac{1}{2}$×5=2.5,BD=2OB,
∴在Rt△OBC中,OB=OC•tan∠ACB=2.5×$\sqrt{3}$=$\frac{5\sqrt{3}}{2}$,
∴BD=2OB=5$\sqrt{3}$.
故选C.
点评 此题考查了菱形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完全这件事的不同办法数是各类不同方法种树的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分别几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分布计数原理,也叫做乘法原理.
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
小王想获得至少30分的加分,那么概率为多少?
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
| 加分 | 人数 |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
11.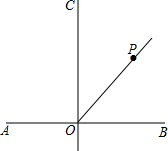 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.(x-2)(x+3)的运算的结果是( )
| A. | x2-6 | B. | x2+6 | C. | x2-5x-6 | D. | x2+x-6 |
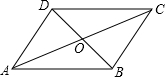 如图,在平行四边形ABCD中,O是对角线AC,BD的交点
如图,在平行四边形ABCD中,O是对角线AC,BD的交点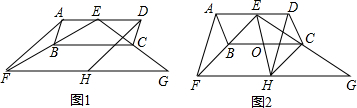
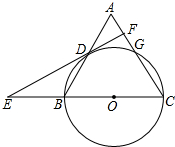 如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.
如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.