题目内容
15.若两个不等实数m,n满足条件:m2-2m-5=0,n2-2n-5=0,则m2+n2的值是14.分析 利用已知等式,可把m、n看作关于方程x2-2x-5=0的两根,根据根与系数的关系得到m+n=2,mn=-5,再利用完全平方公式变形得到m2+n2=(m+n)2-2mn,然后利用整体代入的方法计算即可.
解答 解:∵m2-2m-5=0,n2-2n-5=0,
∴m、n可看作关于方程x2-2x-5=0的两根,
∴m+n=2,mn=-5,
∴m2+n2=(m+n)2-2mn=22-2×(-5)=14.
故答案为14.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
7.物体在前一半路程的速度是6m/s,后一半路程的速度为4m/s,物体运动的平均速度为( )
| A. | 5m/s | B. | 4.8m/s | C. | 17.5m/s | D. | 16.7m/s |
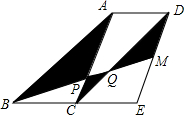 如图,四边形ABCD和四边形ACED都是平行四边形,点M为DE的中点,BM分别交AC和CD于点P,Q.若△ABC的面积为6,则图中阴影部分的面积为7.
如图,四边形ABCD和四边形ACED都是平行四边形,点M为DE的中点,BM分别交AC和CD于点P,Q.若△ABC的面积为6,则图中阴影部分的面积为7. 己知a,b,c在数轴上的位置如图所示.
己知a,b,c在数轴上的位置如图所示.