题目内容
10.如图1,将一条两边互相平行的纸袋折叠.(1)若图中α=70°,则β=55°;
(2)探求图中α与β的数量关系;
(3)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,直接写出此时β的大小.

分析 (1)根据两直线平行,同位角相等,可知∠OAD=α=70°,再利用折叠的性质可知β=55°;
(2)由折叠的性质和平行线的性质可知α+2β=180°;
(3)根据折叠的性质可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,从而可知,∠ACB=90°,从而α=90°,再由(2)中的α+2β=180°,得到β=45°.
解答 解:(1)根据上下边互相平行可知,α=∠OAD(两直线平行,同位角相等),因为α=70°,所以∠OAD=70°.又因为∠OAD+2β=180°,所以β=55°.故答案为:β=55°.
(2)根据上下边互相平行可知,α=∠OAD(两直线平行,同位角相等),又因为∠OAD+2β=180°,所以α+2β=180°.故答案为:α+2β=180°.
(3)根据折叠的性质可知,折叠两次后形成的三个角都相等,根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,从而可知,∠ACB=90°,从而α=90°,再由(2)中的α+2β=180°,得到β=45°.故答案为:β=45°.
点评 本题考查学生对平行线性质和折叠问题的掌握情况,根据实际情况对问题进行解答.学生可以自主动手操作,通过实际操作可以较容易的对问题进行解答.

练习册系列答案
相关题目
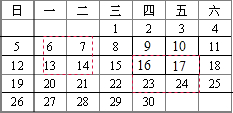 在日历上,我们可以发现其中某些数满足一定的规律.如图是2012年8月份的日历,我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减,例如:7×13-6×14=7,17×23-16×24=7.不难发现,结果都是7.
在日历上,我们可以发现其中某些数满足一定的规律.如图是2012年8月份的日历,我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减,例如:7×13-6×14=7,17×23-16×24=7.不难发现,结果都是7.