题目内容
3.(1)如果欲求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$,可以令x=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$,①
将①式两边乘以$\frac{1}{2}$,得$\frac{1}{2}$x=$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$+$\frac{1}{256}$,②
由②减去①,得x=$\frac{127}{128}$.
(2)用由特殊到一般的方法知:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,则an=a1qn-1(用含a1,q,n的代数式表示),如果这个常数q≠1,那么Sn=a1+a2+a3+…an=Sn=$\frac{{a}_{1}({q}^{n}-1)}{q-1}$或Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$(用含a1,q,n的代数式表示).
(3)已知数列满足(2),且a6-a4=24,a3a5=64,求S8=a1+a2+a3+…a8.
分析 (1)根据题中的提示,可得x的值;
(2)由(1)的方法,依次可以推出a1+a2+a3+…+an的值,注意分两种情况讨论;
(3)由已知条件求出首项和公比,再代入等比数列前n项和公式的答案
解答 解:(1)将①式两边乘以$\frac{1}{2}$,得$\frac{1}{2}$x=$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$+$\frac{1}{256}$,
由②减去①,得x=$\frac{127}{128}$,
故答案为:$\frac{1}{2}$x=$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{128}$+$\frac{1}{256}$,$\frac{127}{128}$;
(2)∵第二项开始每一项与前一项之比的常数为q,
∴an=a1qn-1,
∵Sn=a1+a2+a3+…+an=a1+a1q+a1q2+…+a1qn-1 ①
∴qSn=a1q+a1q2+a1q3+…+a1qn ②
②-①得:Sn=$\frac{{a}_{1}({q}^{n}-1)}{q-1}$或①-②得Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$;
(3)(4)∵a6-a4=24,a3a5=64,
∴a1q5-a1q3=24①,a1q2•a1q4=64②,
解得:$\left\{\begin{array}{l}{{a}_{1=1}}\\{q=2}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=-1}\\{q=-2}\end{array}\right.$,
∴$\frac{1×({2}^{8}-1)}{2-1}$=255或$\frac{-1×(1-{2}^{8})}{1-(-2)}$=85.
点评 此题考查数字的变化规律,找出数字之间的联系,正确判定符号,得出运算规律,解决问题.

 名校课堂系列答案
名校课堂系列答案 如图所示,已知∠1=∠2,∠B=60°,∠ACB=80°,求∠BCD的度数.
如图所示,已知∠1=∠2,∠B=60°,∠ACB=80°,求∠BCD的度数.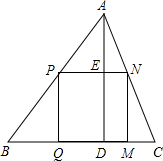 △ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
△ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上. 如图,将△ABC的顶点A沿DE直线折叠,如图,当点A落在原△ABC外部时,探求∠1,∠2与∠A的数量关系.
如图,将△ABC的顶点A沿DE直线折叠,如图,当点A落在原△ABC外部时,探求∠1,∠2与∠A的数量关系.