题目内容
4. 己知a,b,c在数轴上的位置如图所示.
己知a,b,c在数轴上的位置如图所示.(1)若a,b,c满足等式|a-$\frac{3}{2}$|+|b-$\frac{2}{3}$|=-|c+$\frac{5}{2}$|,试求a,b,c的值;
(2)化简:|a+1|-|c-b|+|b-1|;
(3)若a+b+c=0,且b与-1的距离和c与-1的距离相等,求-5a+4b+4c的值.
分析 (1)根据绝对值非负数的性质可求a,b,c的值;
(2)根据绝对值的性质化简即可;
(3)根据b与-1的距离和c与-1的距离相等,可得b-(-1)=-1-c,由于a+b+c=0,把-5a+4b+4c变形即可求解.
解答 解:(1)∵|a-$\frac{3}{2}$|+|b-$\frac{2}{3}$|=-|c+$\frac{5}{2}$|,
∴|a-$\frac{3}{2}$|+|b-$\frac{2}{3}$|+|c+$\frac{5}{2}$|=0,
∴a-$\frac{3}{2}$=0,解得a=$\frac{3}{2}$;
b-$\frac{2}{3}$=0,解得b=$\frac{2}{3}$;
c+$\frac{5}{2}$=0,解得c=-$\frac{5}{2}$;
(2)∵a+1>0,c-b<0,b-1<0,
∴原式=a+1+c-b-b+1
=a-2b+c+2;
(3)由已知得:b+1=-1-c,即b+c=-2,
∵a+b+c=0,即-2+a=0,
∴a=2,
则原式=-10+4(b+c)
=-10-8
=-18.
点评 此题考查了整式的加减,数轴,以及绝对值,弄清题意是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如果有理数a=5.93×1012,则a的整数部分的位数是( )
| A. | 13 | B. | 12 | C. | 14 | D. | 11 |
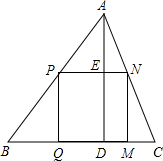 △ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
△ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上. 如图,将△ABC的顶点A沿DE直线折叠,如图,当点A落在原△ABC外部时,探求∠1,∠2与∠A的数量关系.
如图,将△ABC的顶点A沿DE直线折叠,如图,当点A落在原△ABC外部时,探求∠1,∠2与∠A的数量关系.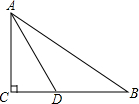 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,AB=10,D在线段BC上,△ACD的面积为9,求证:AD是△ABC的角平分线.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,AB=10,D在线段BC上,△ACD的面积为9,求证:AD是△ABC的角平分线.