题目内容
6．
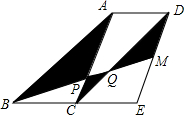如图，四边形ABCD和四边形ACED都是平行四边形，点M为DE的中点，BM分别交AC和CD于点P，Q．若△ABC的面积为6，则图中阴影部分的面积为7．
分析 由四边形ABCD和四边形ACED都是平行四边形，易证得△BCP∽△BDE，△ABP∽△CQP∽△DQM，又由点M为DE的中点，可求得各相似三角形的相似比，继而求得答案．
解答 解：∵四边形ABCD和四边形ACED都是平行四边形，
∴AD=BC=CE，AB∥CD，AC∥DE，
∴△BCP∽△BDE，△ABP∽△CQP∽△DQM，
∴CP：EM=BC：BE=1：2，
∵点M为DE的中点，
∴CP：DM=1：2，
∴CP：AC=CP：DE=1：4，
∵S△ABC=6，
∴S△ABP=$\frac{3}{4}$S△ABC=$\frac{9}{2}$，
∵CP：AP=1：3，
∴S△PCQ=$\frac{1}{9}$S△ABP=$\frac{1}{2}$，
∵CP：DM=1：2，
∴S△DQM=4S△PCQ=2，
∴S阴影=S△ABP+S△PCQ+S△DQM=7．
故答案为：7．
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质．注意相似三角形的面积比等于相似比的平方．
练习册系列答案
阅读快车系列答案
相关题目
17．已知A=a+a2+a3+…+a2014，若a=1，A=m；若a等于-1，A=n，则（ ）
| A． | n+m=0 | B． | n≥m | C． | n+m＜0 | D． | n＜m |
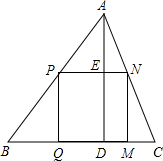△ABC是一块锐角三角形余料，边BC=180mm，高AD=120mm，要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上．
如图，Rt△ABC中，∠C=90°，∠B=2∠A，CD⊥AB于D，则$\frac{AD}{BD}$=3．