题目内容
10.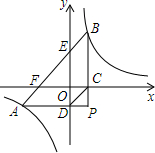 如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点F,E,点B的坐标为(1,3).
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点F,E,点B的坐标为(1,3).(1)k=3;
(2)试说明CD∥BA;
(3)当四边形ABCD的面积和△PCD的面积相等时,求点P的坐标.
分析 (1)把B坐标代入反比例解析式求出k的值即可;
(2)由题意表示出P,D,C,A的坐标,求出两对应边之比,再由夹角相等,利用两边对应边对应成比例且夹角相等的三角形相似得到三角形PDC与三角形PAB相似,进而得出四边形ADCF与四边形DEBC都是平行四边形,利用平行四边形的对边相等即可得证;
(3)由三角形PAB面积的一半等于三角形PCD面积,列出关于a的方程,求出方程的解得到a的值,即可确定出P的坐标.
解答 解:(1)把B(1,3)代入反比例解析式得:k=3;
故答案为:3;
(2)反比例函数解析式为y=$\frac{3}{x}$,
设A点坐标为(a,$\frac{3}{a}$),
∵PB⊥x于点C,PA⊥y于点D,
∴D点坐标为(0,$\frac{3}{a}$),P点坐标为(1,$\frac{3}{a}$),C点坐标为(1,0),
∴PB=3-$\frac{3}{a}$,PC=-$\frac{3}{a}$,PA=1-a,PD=1,
∴$\frac{PC}{PB}$=$\frac{-\frac{3}{a}}{3-\frac{3}{a}}$=$\frac{1}{1-a}$,$\frac{PD}{PA}$=$\frac{1}{1-a}$,
∴$\frac{PC}{PB}$=$\frac{PD}{PA}$,
∴CD∥BA;
(3)∵四边形ABCD的面积=S△PCD,
∴$\frac{1}{2}$•$\frac{1}{2}$•(3-$\frac{3}{a}$)•(1-a)=•1•(-$\frac{3}{a}$),
整理得a2-2a-3=0,解得a1=-1,a2=3(舍去),
∴P点坐标为(1,-3).
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法求反比例函数解析式,坐标与图形性质,平行四边形的判定与性质,以及平行线的判定,熟练掌握平行线的判定是解本题第二问的关键.

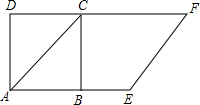 如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.
如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.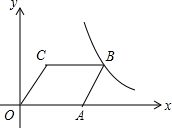 如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.
如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.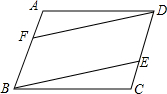 如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.
如图,在?ABCD中,点E、F分别在DC、AB上,DC=3CE,BF=2AF,求证:DF=BF,DF∥BF.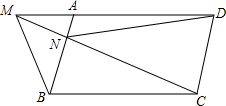 已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.
已知M是?ABCD的DA边的延长线上任一点,连结MC交AB于N,求证:S△MNB=S△AND.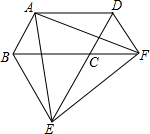 如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.
如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.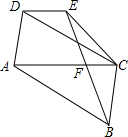 如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.
如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.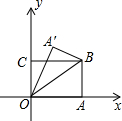 如图,四边形0ABC为矩形,A在x轴上,C在y轴上,B点坐标为(4,3),将△OAB沿OB翻折,A的对应点为A′,0A′交BC于D,则D点的坐标为($\frac{7}{8}$,3).
如图,四边形0ABC为矩形,A在x轴上,C在y轴上,B点坐标为(4,3),将△OAB沿OB翻折,A的对应点为A′,0A′交BC于D,则D点的坐标为($\frac{7}{8}$,3).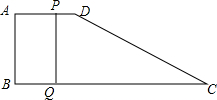 如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动.