题目内容
15.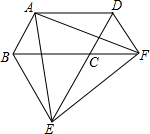 如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.
如图,在平行四边形ABCD中,△BCE、△CDF都是等边三角形,试说明△AEF是等边三角形.
分析 先证明△ABE≌△ADF,再证明△ADF≌△ECF即可解决问题.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠ABC=∠ADC,
∵∠ABE=∠ABC+∠CBE ,∠ADF=∠ADC+∠CDF,
,∠ADF=∠ADC+∠CDF,
∵,△BCE、△CDF都是等边三角形,
∴∠CBE=60°=∠CDF,BE=BC=AD,AB=CD=DF,
∴∠ABE=∠ADF
在△ABE和△ADF中,
$\left\{\begin{array}{l}{BE=AD}\\{∠ABE=∠ADF}\\{AB=DF}\end{array}\right.$,
∴△ABE≌△ADF
∴AE=AF
∵∠ECF=360°-∠BCD-∠BCE-∠DCF=360°-(180°-∠ADC)-60°-60°=∠ADC+60°=∠ADF,
在△ADF和△ECF中,
$\left\{\begin{array}{l}{EC=AD}\\{∠ADF=∠ECF}\\{DF=CF}\end{array}\right.$,
∴△ADF≌△ECF,
∴AF=EF,
∴AE=AF=EF,
∴△AEF是等边三角形.
点评 本题考查平行四边形的性质.等边三角形的判定等知识,解题的关键是正确寻找全等三角形,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
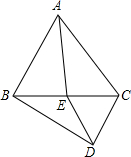 如图所示,△ABC、△DEC是等边三角形.
如图所示,△ABC、△DEC是等边三角形.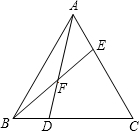 如图,已知△ABC中,AE:EC=1:3,BD:DC=1:2,AD与BE交于点F,求$\frac{EF}{BF}$+$\frac{AF}{DF}$的值.
如图,已知△ABC中,AE:EC=1:3,BD:DC=1:2,AD与BE交于点F,求$\frac{EF}{BF}$+$\frac{AF}{DF}$的值.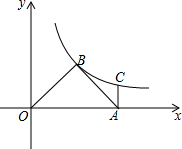 如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.
如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.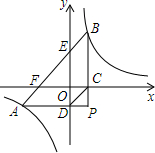 如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点F,E,点B的坐标为(1,3).
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点F,E,点B的坐标为(1,3).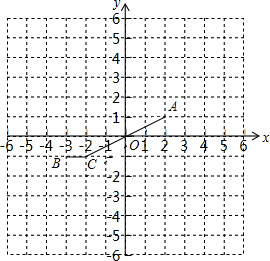 若A、B、C、D四点构成平行四边形A(2,1)、B(-3,1)、C(-2,-1),则顶点D的坐标为(3,1)或(1,1)或(-5,-3).
若A、B、C、D四点构成平行四边形A(2,1)、B(-3,1)、C(-2,-1),则顶点D的坐标为(3,1)或(1,1)或(-5,-3).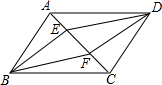 如图,在?ABCD中,点E,F的对角线AC上的两点,且AE=CF,求证:DE=BF,BE=DF.
如图,在?ABCD中,点E,F的对角线AC上的两点,且AE=CF,求证:DE=BF,BE=DF.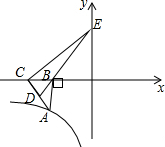 如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴正半轴于点E,双曲线y=$\frac{k}{x}$(x<0)的图象经过点A,S△BEC=8,则k=16.
如图,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线交y轴正半轴于点E,双曲线y=$\frac{k}{x}$(x<0)的图象经过点A,S△BEC=8,则k=16.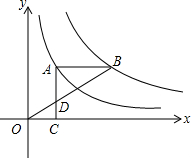 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AC⊥x轴于C.连接OB与AC相交于点D,若AD=2DC.则k的值为6.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AC⊥x轴于C.连接OB与AC相交于点D,若AD=2DC.则k的值为6.