题目内容
2．
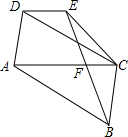如图，在?ABCD中，过点B作BE交对角线AC于点F，且BF=EF，连接DE、CE，求证：AC∥DE．
分析 过点E作EN∥BC，交AC于点M，交AB于点N，先证明△MEF≌△CBF，再证明四边形ADEM是平行四边形即可．
解答 解：如图1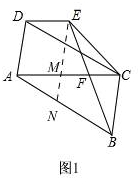
过点E作EN∥BC，交AC于点M，交AB于点N，
在?ABCD中，AD∥BC，
∴BC∥EN，AD=BC，
∴∠MEF=∠FBC，
在△MEF和△CBF中，
$\left\{\begin{array}{l}{∠MEF=∠FBC}\\{EF=BF}\\{∠EFM=∠BFC}\end{array}\right.$，
∴△MEF≌△CBF，
∴BC=EM，
∴AD=EM，
∵AD∥EM，
∴四边形ADEM是平行四边形，
∴DE∥AM，
∴AC∥DE．
点评 此题主要考查平行四边形的性质和全等三角形的证明与运用，熟悉平行四边形的性质，会构造三角形全等并运用于平行四边形的判定是解题的关键．
练习册系列答案
相关题目
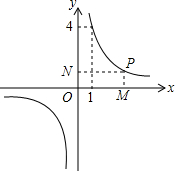如图所示，P是反比例函数y=$\frac{k}{x}$的图象上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为M，N．
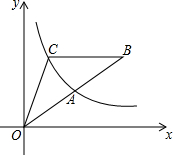如图，点A是反比例函数y=$\frac{k}{x}$的图象上的一点，B是直线OA上的一点，且OA=AB，过点B作x轴的平行线交曲线y=$\frac{k}{x}$于点C，连OC，若S△ABC=9，那么k的值等于6．
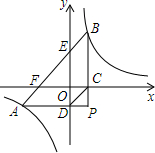如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上，且PB⊥x轴于点C，PA⊥y轴于点D，AB分别与x轴，y轴相交于点F，E，点B的坐标为（1，3）．
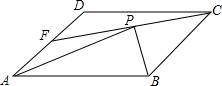在平行四边形ABCD中，F是AD的中点，BP⊥CF交于点P，若AP=2$\sqrt{3}$，求AB的长．
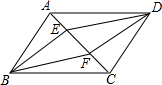如图，在?ABCD中，点E，F的对角线AC上的两点，且AE=CF，求证：DE=BF，BE=DF．
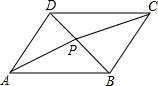如图，点P是?ABCD内的一点，连结AP，BP，CP，DP，若△APB的面积为40cm2，△BPC的面积为25cm2，△CPD的面积为15cm2，则根据题目中所给的条件，能求出△PAD的面积吗？如果能，请你求出△PAD的面积；如果不能，请你说明理由．