题目内容
20.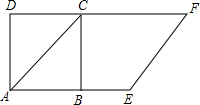 如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.
如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.
分析 由四边形ABCD是正方形,可得AC=$\sqrt{2}$BC,又由菱形的面积为9$\sqrt{2}$cm2,AE=AC,可求得BC的长,继而求得答案.
解答 解:∵四边形ABCD是正方形,
∴∠CAB=45°,
∴AC=$\sqrt{2}$BC,
∵菱形的面积为9$\sqrt{2}$cm2,AE=AC,
∴AE•BC=$\sqrt{2}$BC2=9$\sqrt{2}$,
解得:BC=3,
∴正方形ABCD的面积为:9.
故答案为:9.
点评 此题考查了菱形的性质以及正方形的性质.注意由菱形的面积,求得BC的长是关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
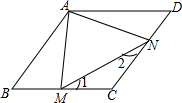 如图,在菱形ABCD中,M、N分别是边BC、CD上的点,且AM=AN=MN=AB,则∠C的度数为100°.
如图,在菱形ABCD中,M、N分别是边BC、CD上的点,且AM=AN=MN=AB,则∠C的度数为100°.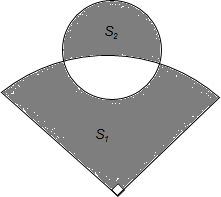 如图,在半径为5,圆心角为90°的扇形中,阴影部分的面积S1;在半径为2的圆中,阴影部分的面积为S2,则S1-S2=$\frac{9}{4}$π(结果保留π).
如图,在半径为5,圆心角为90°的扇形中,阴影部分的面积S1;在半径为2的圆中,阴影部分的面积为S2,则S1-S2=$\frac{9}{4}$π(结果保留π). 如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.
如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.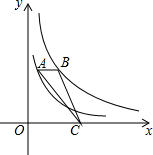 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双AB曲线y=$\frac{5}{x}$上.点C是x轴上一动点.若AB∥x轴.则△ABC的面积为1.5.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双AB曲线y=$\frac{5}{x}$上.点C是x轴上一动点.若AB∥x轴.则△ABC的面积为1.5.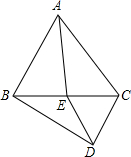 如图所示,△ABC、△DEC是等边三角形.
如图所示,△ABC、△DEC是等边三角形.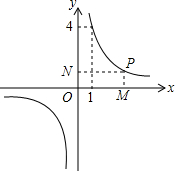 如图所示,P是反比例函数y=$\frac{k}{x}$的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为M,N.
如图所示,P是反比例函数y=$\frac{k}{x}$的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为M,N.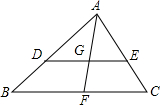 如图,已知AF是△ABC的中线,D、E分别为AB、AC上一点,DE∥BC,DE交AF于G,求证:DG=GF.
如图,已知AF是△ABC的中线,D、E分别为AB、AC上一点,DE∥BC,DE交AF于G,求证:DG=GF.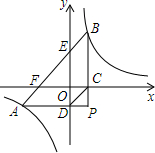 如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点F,E,点B的坐标为(1,3).
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴,y轴相交于点F,E,点B的坐标为(1,3).