题目内容
14.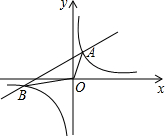 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.
分析 解方程求得交点的横坐标,由直线解析式求得直线与y轴的交点坐标,然后根据△AOB的面积=两个三角形面积的和,列出方程,解方程即可求得.
解答 解:解$\frac{1}{2}$x+2=$\frac{k}{x}$得x1=-2+$\sqrt{2k+4}$,x2=-2-$\sqrt{2k+4}$,
∴A的横坐标为-2+$\sqrt{2k+4}$,B的横坐标为-2-$\sqrt{2k+4}$,
∵直线y=$\frac{1}{2}$x+2,
∴直线y=$\frac{1}{2}$x+2与y轴的交点为(0,2),
∴S△AOB=$\frac{1}{2}$×2×(-2+$\sqrt{2k+4}$)+$\frac{1}{2}$×2×(2+$\sqrt{2k+4}$)=6,
解得k=3.
故答案为3.
点评 本题考查了反比例函数和一次函数的交点问题,解方程求得交点的横坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )
如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )
 如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )
如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )| A. | 20cm | B. | 21cm | C. | 22cm | D. | 23cm |
 如图,两个是同心圆,弦AB与小圆相切于点C,且AB=8cm,则这个环形的面积是16πcm2.
如图,两个是同心圆,弦AB与小圆相切于点C,且AB=8cm,则这个环形的面积是16πcm2.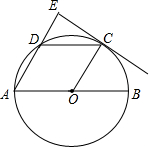 如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$.
如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$. 如图所示,小李决定星期日登A、B、C、D中的某山,打算上午9点由P地出发,尽可能去最远的山,登上山顶后休息一小时,到下午3点以前回到P地.如果去时步行的平均速度为3km/h,返回时步行的平均速度为4km/h.试问小李能登上哪个山顶?(图中数字表示由P地到能登山顶的里程)
如图所示,小李决定星期日登A、B、C、D中的某山,打算上午9点由P地出发,尽可能去最远的山,登上山顶后休息一小时,到下午3点以前回到P地.如果去时步行的平均速度为3km/h,返回时步行的平均速度为4km/h.试问小李能登上哪个山顶?(图中数字表示由P地到能登山顶的里程)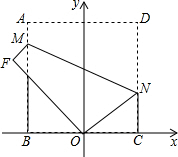 如图,以正方形ABCD的边BC的中点O为原点建立平面直角坐标系,沿过点N(4,3)的一条直线MN进行折叠,点D恰好与点O重合,则直线MN的解析式是y=-$\frac{1}{2}$x+5.
如图,以正方形ABCD的边BC的中点O为原点建立平面直角坐标系,沿过点N(4,3)的一条直线MN进行折叠,点D恰好与点O重合,则直线MN的解析式是y=-$\frac{1}{2}$x+5.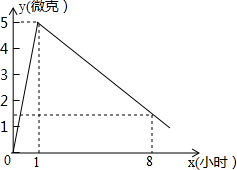 某研究所对某种挥发性有毒液体进行监测,有毒液体的挥发量y(微克)随时间x(小时)的变化如图所示.
某研究所对某种挥发性有毒液体进行监测,有毒液体的挥发量y(微克)随时间x(小时)的变化如图所示.