题目内容
3.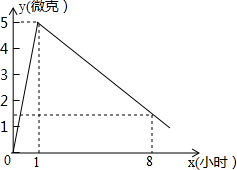 某研究所对某种挥发性有毒液体进行监测,有毒液体的挥发量y(微克)随时间x(小时)的变化如图所示.
某研究所对某种挥发性有毒液体进行监测,有毒液体的挥发量y(微克)随时间x(小时)的变化如图所示.(1)分别求出x≤1,x>1时y与x之间的函数关系式;
(2)从开始监测算起,多少小时后有毒液体不再挥发?
分析 (1)设出y与x之间的函数关系式,结合图象中点的坐标,利用待定系数法即可求出结论;
(2)在x>1时,令y=0,求出x的值,由此得出结论.
解答 解:(1)设当x≤1时,y与x之间的函数关系式为y=k1x+b1;当x>1时,y与x之间的函数关系式为y=k2x+b2.
根据图象中的点的坐标可知:$\left\{\begin{array}{l}{0={b}_{1}}\\{5={k}_{1}+{b}_{1}}\end{array}\right.$和$\left\{\begin{array}{l}{5={k}_{2}+{b}_{2}}\\{1.5=8{k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=5}\\{{b}_{1}=0}\end{array}\right.$和$\left\{\begin{array}{l}{{k}_{2}=-0.5}\\{{b}_{2}=5.5}\end{array}\right.$.
故当x≤1时,y与x之间的函数关系式为y=5x;当x>1时,y与x之间的函数关系式为y=-0.5x+5.5.
(2)当x>1时,令y=0,即-0.5x+5.5=0,
解得:x=11.
答:从开始监测算起,11小时后有毒液体不再挥发.
点评 本题考查了待定系数法求函数的解析式以及解一元一次方程,解题的关键是:(1)结合图象中的点的坐标利用待定系数法求解;(2)在x>1中,令y=0得出关于x的一元一次方程.本题属于基础题,难度不大,解决该类型题目时,结合图象中点的坐标利用待定系数法即可得出结论.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
18.正方形具有而矩形不一定具有的性质是( )
| A. | 四个角相等 | B. | 对角线互相垂直 | C. | 对角互补 | D. | 对角线相等 |
15.已知二元一次方程2x+y=8.
(1)填表:
(2)请写出方程2x+y=8的正整数解;
(3)以表格中的数值x,y作为点的横坐标和纵坐标,在平面直角坐标系内描出各点,再顺次连接各点,得到怎样的图形?
(1)填表:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 12 | 10 | 8 | 6 | 4 |
(3)以表格中的数值x,y作为点的横坐标和纵坐标,在平面直角坐标系内描出各点,再顺次连接各点,得到怎样的图形?
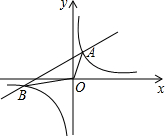 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.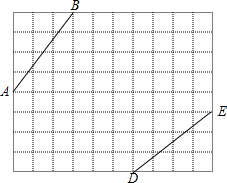 如图所示,是10×8的正方形网格,网格中的每个小正方形的边长都是1,线段AB和线段DE的端点都在小正方形的顶点上.
如图所示,是10×8的正方形网格,网格中的每个小正方形的边长都是1,线段AB和线段DE的端点都在小正方形的顶点上.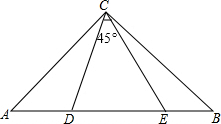 Rt△ABC中,AC=BC,∠DCE=45°,探究DE,BE,AD的关系.
Rt△ABC中,AC=BC,∠DCE=45°,探究DE,BE,AD的关系.