题目内容
6.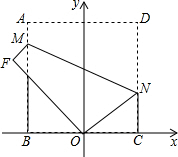 如图,以正方形ABCD的边BC的中点O为原点建立平面直角坐标系,沿过点N(4,3)的一条直线MN进行折叠,点D恰好与点O重合,则直线MN的解析式是y=-$\frac{1}{2}$x+5.
如图,以正方形ABCD的边BC的中点O为原点建立平面直角坐标系,沿过点N(4,3)的一条直线MN进行折叠,点D恰好与点O重合,则直线MN的解析式是y=-$\frac{1}{2}$x+5.
分析 延长NO、AB交于点H,由△ONC≌△OHB得OH=ON,再证明△HMN是等腰三角形,即可求出点M坐标解决问题.
解答 解:如图延长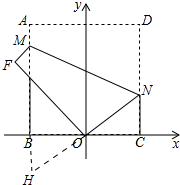 NO、AB交于点H.
NO、AB交于点H.
在RT△ONC中,∵0C=4,NC=3,
∴ON=$\sqrt{O{C}^{2}+C{N}^{2}}$=5,
在△ONC和△OHB中,
$\left\{\begin{array}{l}{∠NOC=∠BOH}\\{∠OCN=∠OBH}\\{OC=OB}\end{array}\right.$,
∴△ONC≌△OHB,
∴ON=OH=5,BH=CN=3,
∵∠MND=∠MNH,AB∥CD,
∴∠HMN=∠MND,
∴∠HMN=∠HNM,
∴HN=HM=10,BM=7,
∴点M(-4,7),设直线MN为y=kx+b,
∴$\left\{\begin{array}{l}{-4k+b=7}\\{4k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=5}\end{array}\right.$.
∴直线MN的解析式为y=-$\frac{1}{2}$x+5.
点评 本题考查翻折变换、待定系数法确定一次函数解析式、全等三角形的判定和性质、勾股定理等知识,解题的关键是发现△HMN是等腰三角形,属于中考常考题型.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
16.若两圆的半径分别是2和4,圆心距为2,则两圆的位置关系为( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 外离 |
18.正方形具有而矩形不一定具有的性质是( )
| A. | 四个角相等 | B. | 对角线互相垂直 | C. | 对角互补 | D. | 对角线相等 |
15.已知二元一次方程2x+y=8.
(1)填表:
(2)请写出方程2x+y=8的正整数解;
(3)以表格中的数值x,y作为点的横坐标和纵坐标,在平面直角坐标系内描出各点,再顺次连接各点,得到怎样的图形?
(1)填表:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 12 | 10 | 8 | 6 | 4 |
(3)以表格中的数值x,y作为点的横坐标和纵坐标,在平面直角坐标系内描出各点,再顺次连接各点,得到怎样的图形?
16.不等式x+1<0的解集在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
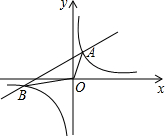 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.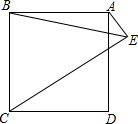 如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.
如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.