题目内容
5. 如图,两个是同心圆,弦AB与小圆相切于点C,且AB=8cm,则这个环形的面积是16πcm2.
如图,两个是同心圆,弦AB与小圆相切于点C,且AB=8cm,则这个环形的面积是16πcm2.
分析 连接OC、OA,构造出Rt△AOC,求出OA2-OC2的值,再乘以π即为环形的面积.
解答  解:连接OC、OA,则OC⊥AB,
解:连接OC、OA,则OC⊥AB,
在Rt△AOC中,
OA2-OC2=AC2=($\frac{1}{2}$AB)2=16cm2,
所以环形的面积为OA2π-OC2π=16πcm2,
故答案为:16πcm2.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
16.若两圆的半径分别是2和4,圆心距为2,则两圆的位置关系为( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 外离 |
20.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知二元一次方程2x+y=8.
(1)填表:
(2)请写出方程2x+y=8的正整数解;
(3)以表格中的数值x,y作为点的横坐标和纵坐标,在平面直角坐标系内描出各点,再顺次连接各点,得到怎样的图形?
(1)填表:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 12 | 10 | 8 | 6 | 4 |
(3)以表格中的数值x,y作为点的横坐标和纵坐标,在平面直角坐标系内描出各点,再顺次连接各点,得到怎样的图形?
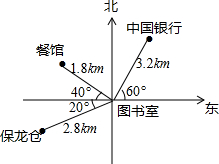 如图,表示的是图书馆、保龙仓、中国银行和餐馆的位置关系.
如图,表示的是图书馆、保龙仓、中国银行和餐馆的位置关系.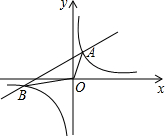 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.