题目内容
9.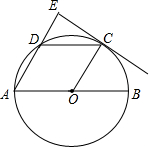 如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$.
如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$.(1)求证:CE是⊙O的切线;
(2)猜想四边形AOCD是什么特殊的四边形,并证明你的猜想.
分析 (1)连接OD,由锐角三角函数得出∠A=60°,证出△OAD是等边三角形,得出∠ADO=∠AOD=60°,再证明△COD是等边三角形,得出∠COD=60°=∠ADO,证出OC∥AE,由已知条件得出CE⊥OC,即可得出结论;
(2)由(1)得:△OAD和△COD是等边三角形,得出OA=AD=OD=CD=OC,即可证出四边形AOCD是菱形.
解答 (1)证明:连接OD,如图所示: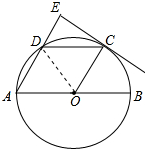
∵tanA=$\sqrt{3}$,
∴∠A=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴∠ADO=∠AOD=60°,
∵CD∥AB,
∴∠ODC=60°,
∵OC=OD,
∴△COD是等边三角形,
∴∠COD=60°=∠ADO,
∴OC∥AE,
∵CE⊥AE,
∴CE⊥OC,
∴CE是⊙O的切线;
(2)解:四边形AOCD是菱形;理由如下:
由(1)得:△OAD和△COD是等边三角形,
∴OA=AD=OD=CD=OC,
∴四边形AOCD是菱形.
点评 本题考查了切线的判定、等边三角形的判定与性质、三角函数、菱形的判定;熟练掌握切线的判定方法,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
20.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.正方形具有而矩形不一定具有的性质是( )
| A. | 四个角相等 | B. | 对角线互相垂直 | C. | 对角互补 | D. | 对角线相等 |
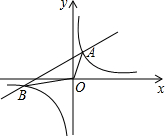 如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.
如图,直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$交于A,B两点,连展A0,B0,所得△A0B面积6,则k的值为3.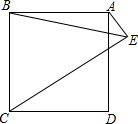 如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.
如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.