题目内容
15.小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则每玩一次应付费3元.(1)请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率;
(2)假设有1000人次玩此游戏,估计游戏设计者可赚多少元?
分析 (1)画树状图展示所有10种等可能的结果数,再找出从开始进入的出入口离开的结果数,然后根据概率公式求解;
(2)利用1000×3减去1000×$\frac{2}{5}$×5可估计游戏设计者可赚的钱.
解答 解:(1)画树状图为:
共有10种等可能的结果数,其中从开始进入的出入口离开的结果数为4,
所以小美玩一次“守株待兔”游戏能得到小兔玩具的概率=$\frac{4}{10}$=$\frac{2}{5}$;
(2)1000×3-1000×$\frac{2}{5}$×5=1000,
所以估计游戏设计者可赚1000元.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.

练习册系列答案
相关题目
8.计算:
(1)(-1)2017-23+(cos68°+$\frac{5}{π}$)0+|3$\sqrt{3}$-8sin60°|;
(2)$\sqrt{2}$cos45°-tan30°•sin60°.
(1)(-1)2017-23+(cos68°+$\frac{5}{π}$)0+|3$\sqrt{3}$-8sin60°|;
(2)$\sqrt{2}$cos45°-tan30°•sin60°.
6.若k为正整数,则2•(-2)2k+(-2)2k+1等于( )
| A. | 0 | B. | 22k+1 | C. | -22k+1 | D. | 22k+2 |
10.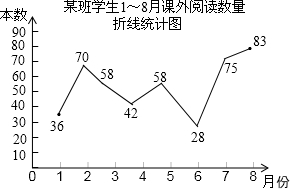 班长统计了今年1~8月“书香校园”活动中全班同学的课外阅读数量是(单位:本),绘制了如图折线统计图,下列说法正确的是( )
班长统计了今年1~8月“书香校园”活动中全班同学的课外阅读数量是(单位:本),绘制了如图折线统计图,下列说法正确的是( )
 班长统计了今年1~8月“书香校园”活动中全班同学的课外阅读数量是(单位:本),绘制了如图折线统计图,下列说法正确的是( )
班长统计了今年1~8月“书香校园”活动中全班同学的课外阅读数量是(单位:本),绘制了如图折线统计图,下列说法正确的是( )| A. | 平均数是45 | B. | 众数是42 | C. | 中位数是58 | D. | 方差小于10 |
4.2617与8213的大小关系是( )
| A. | 2617>8213 | B. | 2617=8213 | C. | 2617<8213 | D. | 不能判定 |
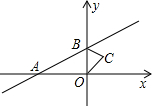 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).
如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-4,-3)或(2,3).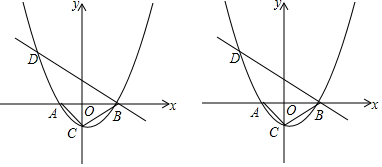
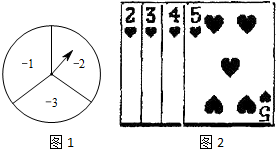 图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.
图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.